L'algebra dei ket conosce l'Analisi di Fourier

venerdì, Maggio 1st, 2020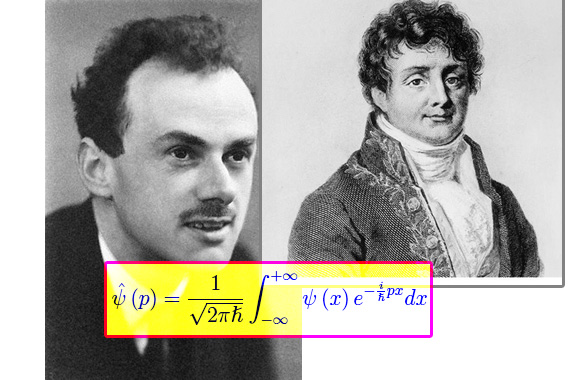

particella,meccanica quantistica,problemi unidimensionali,ket,bra,Dirac,Fourier

Ulteriore aggiornamento del file sui problemi unidimensionali in Meccanica quantistica. L'aggiornamento riguarda il cambiamento di base dalla base delle coordinate {|x>} alla base degli impulsi {|p>}. Notiamo che ciò vale in generale, e non solo nel caso della particella libera. Siamo abituati a pensare alla matrice di passaggio da una base all'altra (matrice unitaria, in quanto le basi sono ortonormali nello spazio di Hilbert L²(-oo,+oo)). Ma lo spazio vettoriale in questione ha dimensione infinita non numerabile (ovviamente si può generalizzare la nozione di matrice, portandola nel continuo). Utilizzando la notazione di Dirac e le proprietà di completezza dei singoli sistemi di vettori di base, si scopre un'importante proprietà: la funzione d'onda nel dominio degli impulsi è la trasformata di Fourier della funzione d'onda nello spazio delle coordinate.
(altro…)

Posted in Meccanica Quantistica | No Comments »

[¯|¯] Le violente oscillazioni della parte reale e della parte immaginaria della zeta di Riemann

lunedì, Gennaio 22nd, 2018

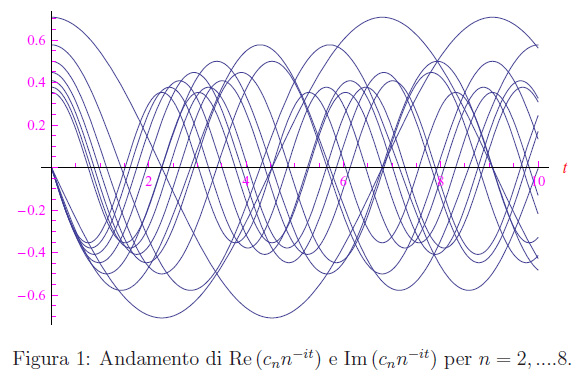
congettura di riemann,zeri non banali,zeta di riemann,fourier

Forse l' analisi di Fourier potrebbe dirci qualcosa sulla congettura di Riemann. Ci riferiamo in particolare alle rapide oscillazioni della parte reale e della parte immaginaria della restrizione della funzione zeta lungo la linea critica. Le oscillazioni sono infatti dovute a termini del tipo n^-it, come mostrato nella figura al top. Nella figura seguente, invece, riportiamo il grafico di alcuni termini della serie di Dirichlet: