Punto base e inviluppo (Base point and envelope)

sabato, Dicembre 26th, 2020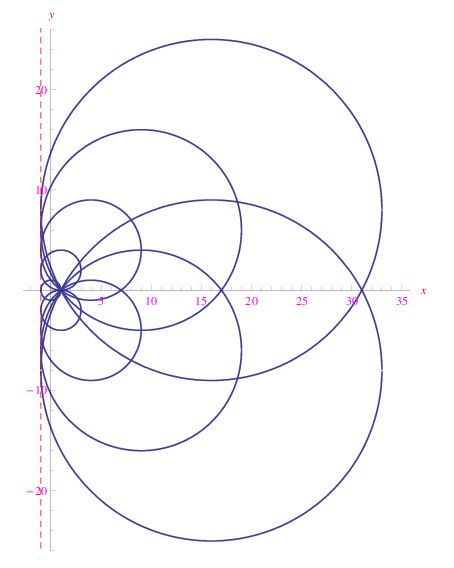

inviluppo,punto base,famiglia di curve piane — **Fig. 1**

Esercizio

Soluzione
Denotiamo con γ_λ la singola circonferenza. Ricordiamo dalla Geometria analitica che la generica equazione di una circonferenza di centro (ξ,η) e raggio R, è:

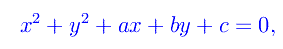
dove

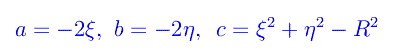
Ne segue che nel nostro caso è

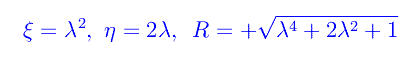
Ora poniamo

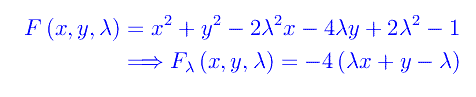
da cui il sistema

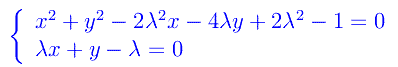
Se nella seconda poniamo x=1 si ha y=0, cioè la soluzione (1,0), e questa verifica anche la prima equazione. Abbiamo perciò trovato il punto base (1,0). Scartando tale soluzione (cioè x diverso da 1) proviamo con x=-1, per cui la seconda restituisce y=2λ. Ponendo nella prima x=-1,y=2λ si perviene a una identità, i.e. abbiamo trovato la soluzione

che è manifestamente una rappresentazione parametrica della retta x+1. Ne concludiamo che quest'ultima è l'inviluppo della famiglia assegnata, come mostrato in fig. 1.

(altro…)

Posted in Geometria differenziale | No Comments »

Curva discriminante di una famiglia di curve piane (Discriminant curve of a family of plane curves)

giovedì, Dicembre 24th, 2020

inviluppo,famiglia di curve piane,curva discriminante

Abbiamo completamente rifatto la lezione sull'inviluppo di una famiglia di curve piane, introducendo l'importante nozione di curva discriminante. L'esistenza di tale luogo geometrico deriva dal rilassamento delle condizioni che compongono le ipotesi del famoso Teorema del Dini, per cui risolvendo l'appropriato sistema di equazione, ci si aspetta la comparsa di luoghi estranei ossia non necessariamente curve inviluppo. Abbiamo esaminato l'esistenza dei famigerati punti base, ora cerchiamo di capire i luogi dei punti singolari.

Scarica la lezione in pdf
(altro…)