Esercizio svolto sul metodo di variazione delle costanti arbitrarie (equazioni differenziali)

lunedì, Maggio 25th, 2020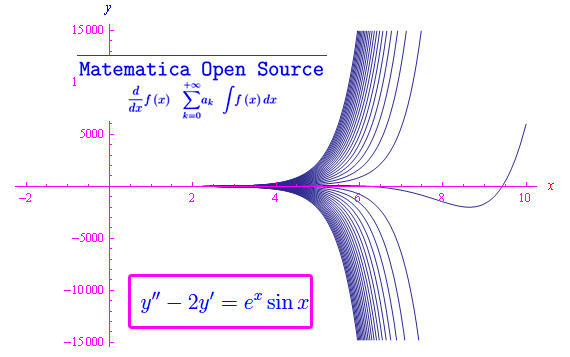

equazioni differenziali,metodo di variazione delle costanti arbitrarie,metodo di lagrange — **Fig. 1**

Assegnata l'equazione differenziale rappresentata in fig. 1, si determini un integrale particolare applicando il metodo di Lagrange

Soluzione
Dobbiamo innanzitutto trovare un sistema fondamentale di integrali dell'equazione omogenea

la cui equazione caratteristica

ammette una coppia di radici reali e distinte: λ₁=0,λ₂=2. Ne seguono gli integrali fondamentali:

(altro…)

Posted in Analisi Matematica II | No Comments »

Mathematica e le soluzioni in forma implicita di equazioni differenziali a variabili separabili

venerdì, Aprile 3rd, 2020

mathematica,equazioni differenziali,variabili separabili

Attenzione ad usare un software del tipo Mathematica per le equazioni differenziali. Proponiamo una equazione differenziale del primo ordine, integrabile per separazione di variabili, ma il cui integrale generale compare in forma implicita. Mathematica forza la soluzione con la funzione ProductLog. Tuttavia, alcuni rami delle soluzioni non sono accettabili.
(altro…)