Densità di corrente di neutroni. Equazione del bilancio

sabato, Novembre 21st, 2020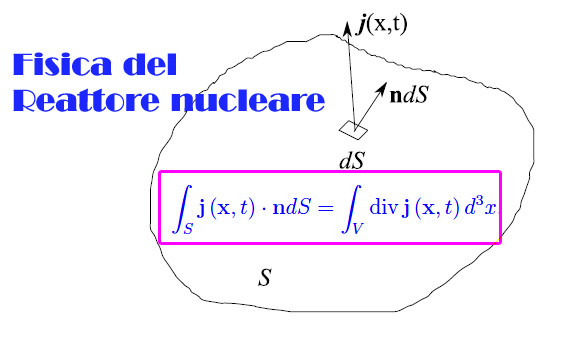

Nel numero precedente abbiamo definito il flusso di neutroni Φ(x,t) come il numero di neutroni che attraversano l'unità di superficie nell'unità di tempo. Possiamo dunque associare a tale campo scalare la grandezza vettoriale densità di corrente j(x,t). Come è noto, si tratta di un procedimento standard applicabile in tutti quei casi in cui si ha una densità di grandezza fisica G(x,t) a cui è possibile associare una densità di corrente. Introducendo una velocità di creazione/assorbimento di neutroni si perviene facilmente all'equazione del bilancio che è una generalizzazione della ben nota equazione di continuità (quest'ultima esprime la conservazione della grandezza in esame).
Tale equazione è scritta in forma integrale, ma applicando il teorema della divergenza si perviene a un'equazione differenziale che esprime localmente il bilancio tra neutroni entranti/uscenti e creati/assorbiti.

(altro…)

Posted in Fisica del Reattore nucleare | No Comments »

Mancano oltre 1800 contagiati/giorno (assumiamo il tempo di guarigione = white noise)

domenica, Aprile 26th, 2020

coronavirus,contagiati,morti,attualmente positivi,equazione del bilancio

In quest'articolo cerchiamo di migliorare il tiro raggiunto nel numero precedente, in cui avevamo assunto costanti il tempo di guarigione e il tempo di decesso. In realtà, avevamo eseguito una media d'insieme e non una media temporale, dando per buona l'ergodicità del sistema dinamico in istudio.

Ora invece, supponiamo variabili le predette grandezze. Nello specifico si tratta di variabili aleatorie ben modellizzabili da un white noise. Come è noto, quest'ultimo è di facile implementazione nell'ambiente di calcolo Mathematica.
Le conclusioni sono del medesimo ordine di grandezza delle precedenti.
(altro…)