Dimostrazione per assurdo del Teorema di unicità del limite
mercoledì, Febbraio 10th, 2016
Oltre alla consueta dimostrazione del Teorema di unicità del limite, quest'articolo contiene una routine in Mathematica per generare una istruttiva animazione grafica per la predetta dimostrazione.
In addition to the usual proof of the Theorem on uniqueness of limits, this article contains a routine in Mathematica to generate an instructive graphic animation for the aforementioned demonstration.
Se f è una funzione reale definita in X sottoinsieme del campo reale e x0 un punto di accumulazione (al finito o all'infinito) per X.
Definizione
Si dice che f è regolare in x0 se è ivi dotata di limite (infinito o infinito). Nel caso contrario, si dice che è f è non regolare in x0.
Nel caso di non regolarità è consuetudine dire, sia pur impropriamente, che in x0 il limite di f non esiste. Per le funzioni regolari, sussiste il teorema di unicità del limite:
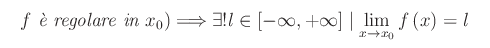
Dimostrazione.
Procediamo per assurdo, negando la tesi (senza perdita di generalità supponiamo che x0 sia di accumulazione al finito e che la funzione sia convergente):
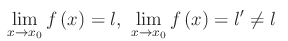
(altro…)



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











