Funzione convergente in modulo, ma non implica necessariamente la convergenza

lunedì, Febbraio 15th, 2021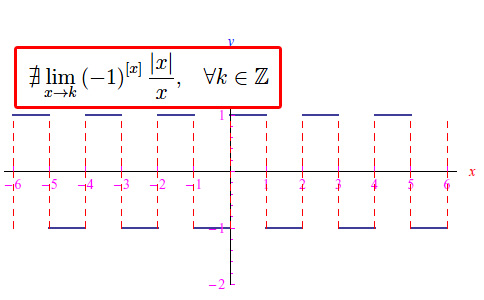

convergenza,convergenza in modulo,limite — **Fig. 1**

Per una funzione che tende a un limite finito (ovvero che converge) ci si può chiedere: converge anche in modulo?. Cioè, il valore assoluto della funzione converge? Intanto dimostriamo la proposizione inversa, ossia se la funzione converge a un limite L, il suo valore assoluto converge al valore assoluto del limite (|L|). Ma non sempre è vero il viceversa, ad eccezione del caso ovvio L=0 (cioè quando la funzione è infinitesima per x che tende al punto di accumulazione considerato). Proponiamo un controesempio (fig. 1) di una funzione convergente in modulo ma che non converge ad alcun limite.

Scarica la lezione in pdf
(altro…)