[¯|¯] Rotore di un campo vettoriale
sabato, Novembre 5th, 2016
Negli ultimi esercizi abbiamo esaminato la nozione di integrabilità di una forma differenziale lineare, per poi vedere alcune applicazioni alla fisica, come ad esempio il lavoro eseguito da un campo di forze
Veniamo ora ad una importante nozione di analisi vettoriale, ovvero il rotore di un campo vettoriale. Come è noto dalla teoria, sotto opportune ipotesi, l'annullarsi del rotore (in tal caso il campo si dice irrotazionale) è una condizione necessaria e sufficiente affinché il campo derivi da un potenziale (campo conservativo).
Esercizio
È irrotazionale il campo
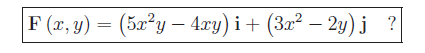



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











