[¯|¯] Il cammino di integrazione è un arco di elica cilindrica (integrale curvilineo)
venerdì, Novembre 11th, 2016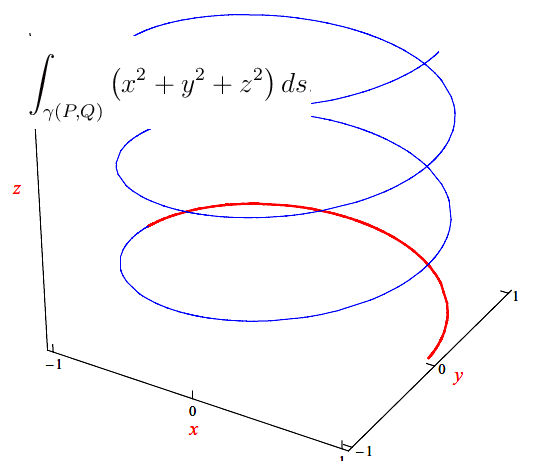
Fig. 1. Cammino di integrazione per l'integrale proposto
Esercizio
Calcolare l'integrale curvilineo:
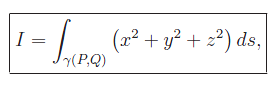
dove il cammino di integrazione è l'arco di elica cilindrica
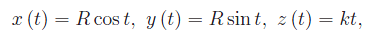
di estremi P(R,0,0) e Q(-R,0,k*π) (cfr fig. 1)
Soluzione
È facile persuadersi che gli estremi P e Q del cammino di integrazione corrispondono rispettivamente ai valori t=0 e t=π del parametro, per cui la rappresentazione parametrica va completata in
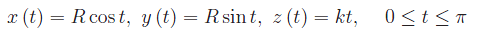
Calcoliamo innanzitutto la funzione:
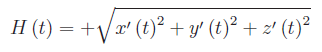
Le derivate delle funzioni x(t),y(t) e z(t) sono
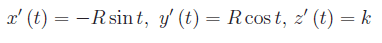
onde
Quindi
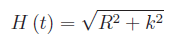
(altro…)
Congettura di Riemann
Trasformata discreta di Fourier
Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier 
Infinitesimi ed infiniti
Limiti notevoli
Punti di discontinuità
Misura di Peano Jordan
Eserciziario sugli integrali
Differenziabilità 
Differenziabilità (2)
Esercizi sui limiti
Appunti sulle derivate
Studio della funzione
Esercizi sugli integrali indefiniti
Algebra lineare
Analisi Matematica 2
Analisi funzionale
Entanglement quantistico
Spazio complesso
Biliardo di Novikov
Intro alla Meccanica quantistica
Entanglement Quantistico
