» Esercizi svolti di Matematica e Fisica

[¯|¯] Omomorfismi ed endomorfismi in ambiente Mathematica

giovedì, Dicembre 15th, 2016

Fondamentalmente, un omomorfismo è una funzione vettoriale lineare. Riferiamoci, in particolare, agli endomorfismi. Ad esempio:

Qui abbiamo inserito il blocco di variabili indipendenti in una lista che Mathematica interpreta alla stregua di un vettore. Definiamo ora gli elementi della base canonica di R^3:

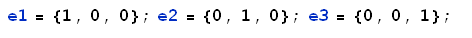
Quindi determiniamo i trasformati di tali vettori attraverso A

Per definizione di matrice rappresentativa di un endomorfismo, deve essere:
(altro…)

---

Posted in Algebra Lineare, Mathematica, Software | No Comments »

[¯|¯] Rango e nullità di un omomorfismo

mercoledì, Dicembre 14th, 2016

---

Esercizio
Assegnato l'omomorfismo

determinarne rango e nullità.

---

Soluzione

Il rango R(A) è per definizione

essendo A(R⁴) l'immagine di R⁴ attraverso A. Risulta:

dove {e_i} è la base canonica di R⁴:

mentre L denota l'operazione di inviluppo lineare. I trasformati dei vettori di base sono:

Si noti che tali vettori sono scritti nella base canonica di R³:

(altro…)

---

Posted in Algebra Lineare, Applicazioni lineari, Matrici e determinanti, Sistemi di equazioni lineari | No Comments »