[¯|¯] Valor medio e valore efficace di una funzione

sabato, Marzo 4th, 2017

analisi funzionale,disuguaglianza di Schwartz,valor medio,valore efficace

Generalizziamo le nozioni esposte nel post precedente.

Assegnato l'intervallo [a,b] quale sottoinsieme di R, poniamo

Come è noto, C([a,b]) assume la struttura di spazio vettoriale su R, introducendo le usuali leggi di composizione:

e relativi assiomi. Tale spazio vettoriale può essere strutturato come spazio euclideo introducendo la forma bilineare:

che verifica gli assiomi di prodotto interno (o prodotto scalare). È facile persuadersi che tali assiomi sono automaticamente verificati dalla seguente forma:

D'altra parte tale definizione è ben posta, giacché la continuità delle funzioni f e g garantisce l'esistenza dell'integrale definito che compare a secondo membro. Si osservi che tale forma definisce il prodotto scalare standard, in quanto è la naturale generalizzazione al continuno del prodotto scalare standard di uno spazio euclideo n-dimensionale

poiché la variabile discreta k viene rimpiazzata dalla variabile continua x. L'introduzione del prodotto scalare ci permette di definire ortogonalità e lunghezza (norma) degli elementi di C([a,b]):

Come è ben noto dall'analisi funzionale, per definire una metrica (i.e. funzione distanza) non è necessario introdurre un prodotto scalare. È però sufficiente; infatti è facile convincersi che la grandezza

verifica gli assiomi della funzione distanza. Per inciso, ancora una volta siamo in presenza di una generalizzazione al continuo. Infatti, in uno spazio euclideo n-dimensionale, la distanza tra due punti la cui posizione è definita dai vettori:

che ammette l'ovvia generalizzazione al continuo:
analisi funzionale,disuguaglianza di Schwartz,valor medio,valore efficace

Ciò premesso, la disuguaglianza di Schwartz lega il valore assoluto del prodotto scalare di due vettori alle rispettive norme. Sussiste infatti il seguente teorema di cui omettiamo la dimostrazione:
Teorema (Disuguaglianza di Schwartz)
analisi funzionale,disuguaglianza di Schwartz,valor medio,valore efficace

In particolare

La seconda parte del teorema è interessante, nel senso che vale l'uguaglianza solo se uno dei due vettori è il vettore nullo, oppure nel caso di parallelismo di f e g. Consideriamo ora la media integrale di f in [a,b]:

che chiamiamo semplicemente valore medio di f. Per il teorema della media:

Definizione 1
Chiamiamo valore efficace di f in [a,b] il numero reale non negativo

Da tale definizione si ha la seguente relazione

(altro…)

Posted in Analisi Funzionale | No Comments »

[¯|¯] Appunti di Analisi funzionale

domenica, Novembre 20th, 2016

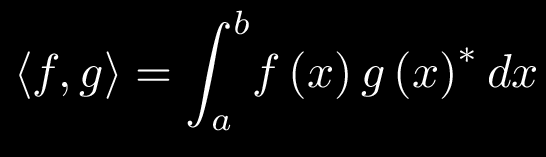
analisi funzionale,spazi di hilbert, spazi di banach, norma,metrica,prodotto scalare

Anche se è incompleto, pubblichiamo ugualmente questo file che può essere trattato alla stregua di un handbook, anche se per ora contiene ben 120 pagine. Si parte dalla definizione di spazio topologico, passando poi per gli spazi con misura (per ora solo quella di Peano - Jordan e non di Lebesgue). Quindi si affronta la questione degli spazi metrici, spazi vettoriali normati con la spinosa questione della completezza, finendo negli spazi di Banach, spazi pre-hilbertiani e spazi di Hilbert.

Scarica il file in pdf