[¯|¯] Le funzioni circolari intere

Luglio 22nd, 2015 | by extrabyte |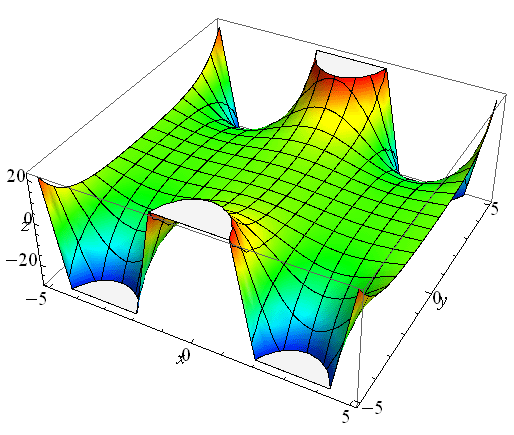

analisi complessa, funzioni circolari intere — **Grafico della parte reale della funzione complessa cos(z che è data da cos(x)*cosh(y)**

Negli appunti di oggi trattiamo le funzioni circolari intere, ovvero l'estensione al campo complesso delle funzioni circolari sin(x) e cos(x).

Il nostro punto di partenza è la formula di Eulero che ci consentirà di esprimere le funzioni circolari come combinazione lineare di esponenziali immaginari. Da qui apparirà poi naturale estendere tali funzioni al campo complesso. Dimostreremo poi l'olomorfia di tali funzioni su tutto il campo complesso. Notevole, infine, ci appariranno la parte reale e la parte immaginaria di tali funzioni, quale prodotto di funzioni iperboliche e funzioni circolari.

Funzioni circolari intere

No TweetBacks yet. (Be the first to Tweet this post)