[¯|¯] Funzioni reali di una variabile reale (Lezione n. 1 di Analisi Matematica 1)
Settembre 12th, 2014 | by extrabyte |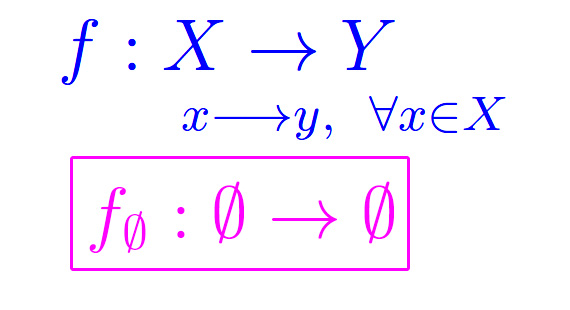
Siano X e Y due insiemi non vuoti.
Definizione
Un'applicazione di X in Y è una legge che ad ogni elemento x appartenente ad X associa univocamente un elemento y dll'insieme Y.
Indicando con f tale applicazione, scriviamo:

e diremo che f è una funzione definita in X e a valori in Y. Al posto della relazione precedente si usa spesso la notazione simbolica:

Per quanto detto, a un generico x di X corrisponde univocamente un elemento y di Y. Per esprimere ciò, scriviamo:

dove f(x) è il valore assunto dalla funzione f in x.
Dalla univocità della predetta corrispondenza

In altri termini, a un assegnato x1 di X, non possono corrispondere più valori di y di Y. Una funzione definita in questo modo, si dice a un sol valore o monodroma. Di contro, si possono definire funzioni a più valori o polidrome. In questi appunti, consideriamo esclusivamente funzioni a un sol valore.
Per quanto visto, una funzione f:X->Y è un'applicazione di X in Y. Resta poi definito il seguente sottoinsieme di Y:

che si chiama immagine di X mediante f.
Osservazione
Il caso speciale

definisce la funzione vuota (seconda formula, fig. 1).
Tags: analisi matematica, applicazione, Funzioni reali di una variabile reale
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico












5 Trackback(s)