Momento della quantità di moto di un punto materiale
Giugno 2nd, 2020 | by Marcello Colozzo |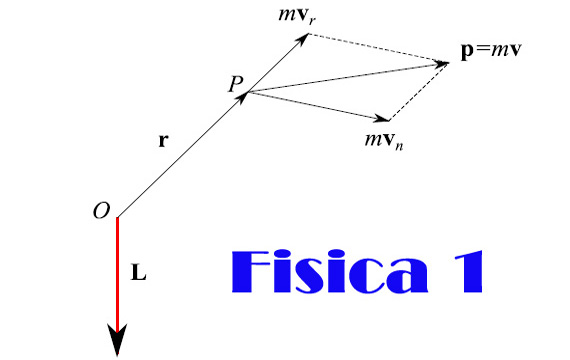
Consideriamo il moto di un punto materiale di massa m rispetto a un assegnato sistema di riferimento inerziale. Come sappiamo, la quantità di moto è

ed è un vettore applicato nella posizione assunta dal punto medesimo. A tale vettore applicato, possiamo naturalmente applicare le nozioni viste nella lezione precedente. Precisamente, il momento della quantità di moto o momento angolare rispetto a un punto O, è

dove r è il vettore posizione del punto di applicazione P rispetto al punto O (non è detto che quest'ultimo sia necessariamente l'origine del sistema di riferimento). Possiamo immaginare di scomporre il vettore quantità di moto nella direzione radiale r e in quella normale, rispettivamente (fig. 1).

per cui

Dal momento che r e vn sono ortogonali:

Ne consegue che al momento angolare contribuisce unicamente la componente normale della velocità del punto materiale.
No TweetBacks yet. (Be the first to Tweet this post)
Articoli correlati



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











