[¯|¯] Definizione assiomatica di equazione differenziale ordinaria

Agosto 31st, 2017 | by Marcello Colozzo |

Nella lezione precedente abbiamo esaminato la genesi per così dire, fisica, delle equazioni differenziali. Passiamo ora alla definizione assiomatica di tale importante ente matematico.
Definizione

Dicesi equazione differenziale ordinaria di ordine n, un'equazione che stabilisce un legame funzionale tra una funzione reale y=y(x) e le sue derivate fino all'ordine n, in cui la funzione y(x) compare come incognita. Quindi:

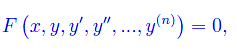
Definizione assiomatica di equazione differenziale ordinaria

Definizione assiomatica di equazione differenziale ordinaria

essendo F una funzione reale assegnata e definita in un sottoinsieme A di Rⁿ⁺².
Osservazione 1
L'equazione differenziale scritta sopra è espressa nella notazione apicale di Lagrange. Nella notazione di Leibnitz si scrive:

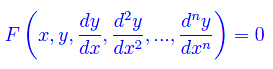
Definizione assiomatica di equazione differenziale ordinaria

Osservazione 2

L'ordine di un'equazione differenziale è l'ordine massimo della derivata della funzione incognita.

Ad esempio, l'equazione differenziale:
Definizione assiomatica di equazione differenziale ordinaria

L'equazione differenziale:
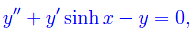
Definizione assiomatica di equazione differenziale ordinaria

è del secondo ordine, come anche l'equazione differenziale
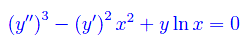
Definizione assiomatica di equazione differenziale ordinaria

Definizione

Un integrale dell'equazione differenziale scritta più sopra è una funzione

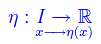
derivabile n volte in I e tale

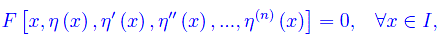
Definizione assiomatica di equazione differenziale ordinaria

essendo I un intervallo non vuoto di R.
Definizione
Una curva integrale dell'equazione differenziale data è il diagramma cartesiano di un qualunque integrale η(x). Cioè:

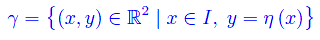
Sostienici

continua in pdf

Indice delle lezioni

No TweetBacks yet. (Be the first to Tweet this post)