[¯|¯] Un "quasi" studio di funzione
Gennaio 14th, 2017 | by Marcello Colozzo |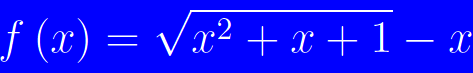
Fig. 1
Studiare il comportamento della funzione illustrata in fig. 1, agli estremi del suo campo di esistenza.
Soluzione
Dal momento che
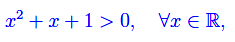
si ha che la funzione è definita in (-oo,+oo). Il limite per x->-oo è immediato
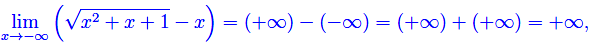
cioè la funzione diverge positivamente per x->-oo. Passiamo al limite per x->+oo:
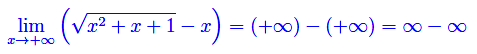
Per risolvere tale forma indeterminata, riscriviamo la funzione
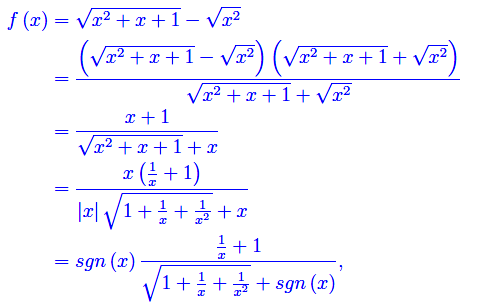
dove sgn(x) è la funzione signum.
Quindi:
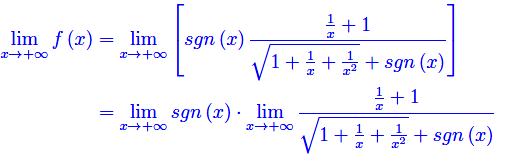
Risulta
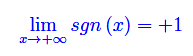
e
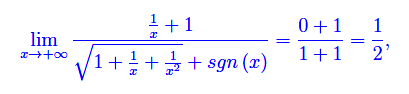
onde
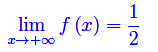
Cioè per x->+oo la funzione è convergente e il limite vale 1/2. Geometricamente, significa che la retta 2y-1=0 è asintoto orizzontale a destra per il grafico della funzione.
No TweetBacks yet. (Be the first to Tweet this post)
Articoli correlati



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











