[¯|¯] Campo di forze sinusolidamente variabile in funzione delle coordinate spaziali

Novembre 7th, 2016 | by Marcello Colozzo |

campi conservativi,potenziale,energia potenziale,lavoro meccanico,integrale curvilineo


Un punto materiale è sottoposto al seguente campo di forze:

campi conservativi,potenziale,energia potenziale,lavoro meccanico,integrale curvilineo

dove le varie grandezze sono espresse nelle appropriate unità di misura. Quanto vale il lavoro compiuto dal campo per spostare la particella da O(0,0) a P(1,1) lungo la curva y=x^(1/2) ?

Soluzione
Scriviamo le componenti cartesiane della forza F:

campi conservativi,potenziale,energia potenziale,lavoro meccanico,integrale curvilineo

Abbiamo
campi conservativi,potenziale,energia potenziale,lavoro meccanico,integrale curvilineo










Ne consegue che il campo non è conservativo, e il lavoro va calcolato tramite integrazione lungo la traiettoria:
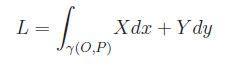
campi conservativi,potenziale,energia potenziale,lavoro meccanico,integrale curvilineo

Continua a leggere in pdf

No TweetBacks yet. (Be the first to Tweet this post)

Tags: , , , ,

Articoli correlati

Commenta l'esercizio