Serie di funzioni non uniformemente convergente, ma con somma continua

Novembre 10th, 2021 | by Marcello Colozzo |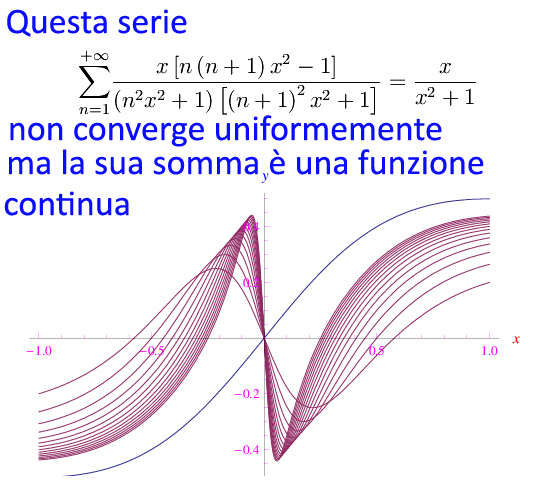

Il seguente esercizio mosta la sufficienza e non la necessità della uniforme convergenza di una serie affinché la somma sia un funzione continua, come stabilito dal teorema della continuità.
Poniamo

che sono manifestamente continue in (-oo,+oo). In fig.

il grafico di alcune di tali funzioni. La somma parziale di ordine 1 è banalmente

Allo scopo di ottenere un'espressione valida per ogni ordine N, decomponiamo il secondo membro in frazioni semplici:

che restituisce il sistema di equazioni lineari

che ammette l'unica soluzione

Con ovvio significato dei simboli

Segue facilmente la somma parziale di ordine N

Dunque la serie converge e la sua somma è

manifestamente continua in (-8,+8). Vediamo se la convergenza è uniforme. Deve essere

Cioè

che per x=0 è verificata per ogni N. Per x diverso da zero

da cui vediamo l'estrremo superiore dell'insieme dei valori assunti dall'indice ν_ε(x) non è limitato superiormente, da cui la non uniformità della convergenza della serie, mentre la sua somma è una funzione continua. In fig. 1 riportiamo il grafico della funzione assieme a quello di alcune somme parziali.

Indice delle lezioni/esercizi

No TweetBacks yet. (Be the first to Tweet this post)