Serie di funzioni. Convergenza puntuale e convergenza uniforme |

Serie di funzioni. Convergenza puntuale e convergenza uniforme

Novembre 3rd, 2021 | by Marcello Colozzo |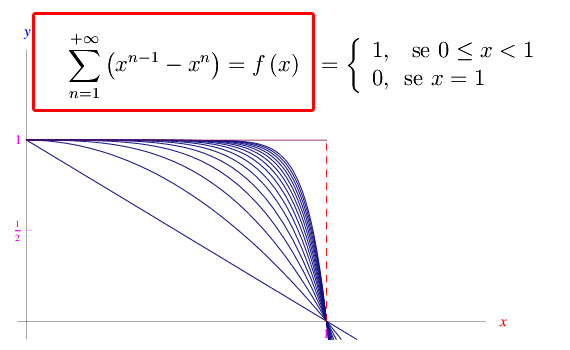

serie di funzioni,convergenza puntuale, convergenza uniforme — **Fig. 1**

Fino a questo momento abbiamo considerato serie numeriche; precisamente, a una successione di elementi di R:

possiamo associare la serie numerica

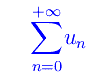
Nulla ci impedisce di generalizzare tale nozione alle funzioni. A tale scopo, consideriamo una successione di funzioni reali della variabile reale x:

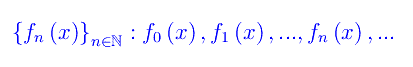
definite in un assegnato insieme X (sottoinsieme di R). A tale successione possiamo associare la serie di funzioni

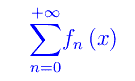
Definizione
La serie di funzioni (v. eq. sopra) è convergente nell'insieme X se comunque prendiamo x₀ in X, è convergente la serie numerica

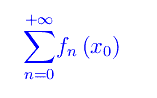
Ne segue che per ogni x appartenente a X

che definisce univocamente in X la funzione f(x) quale somma della serie data. Quindi, per un assegnato x:

dove non abbiamo fatto altro che applicare la definizione di limite alla successione delle somme parziali {S_N(x)}. Notiamo tuttavia che l'indice ν_ε viene a dipendere oltre che da ε, dal punto x. Ciò implica che per un assegnato ε, è definita la funzione:

In tal modo riscriviamo la definizione di limite:

È possibile svincolarsi da x? Per rispondere a tale quesito, consideriamo il codominio della predetta funzione, ovvero l'immagine di X attraverso ν_ε

Se riesce

allora

Cioè abbiamo un unico indice che dipende solo da epsilon;. In tal caso si dice che la serie è uniformemente convergente. Se, invece, il codominio I non è limitato superiormente i.e. supI=+oo, allora non è possibile svincolarsi da x e si dice che si ha convergenza puntuale (o puntiforme) o più semplicemente, convergenza.
Quanto appena esposto, si riformula efficacemente in termini di resto di ordine N della serie assegnata. In generale:

Ad esempio, consideriamo in X=[0,1] la serie

Posto

Vediamo che

cioè una successione di polinomi. La somma parziale di ordine N si scrive:

Cioè

Per calcolare

è preferibile esplicitare dapprima il valore della somma parziale in x=1:

Ne segue

Di contro

In definitiva, la serie è convergente in X

con

Cioè la somma della serie assegnata è una funzione che presenta una discontinuità di prima specie in x=1. Per vedere se la convergenza è uniforme consideriamo il resto di ordine N: