» Esercizi svolti di Matematica e Fisica

Criterio della radice e suo corollario

Criterio della radice

Dim.

Ma pⁿ è il termine n-esimo di una serie geometrica di ragione < 1
da cui l'assoluta convergenza della serie data, in virtù del criterio di confronto. Proviamo la seconda affermazione:

onde la non convergenza della serie data, in virtù di un corollario dimostrato in questa lezione.

Negli esercizi risulta utile il seguente corollario, che però è inapplicabile per l=1.

Corollario

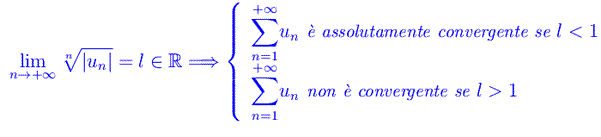
Dim.

Se l < 1, dalla definizione di limite di una successione:

da cui l'assoluta convergenza della serie data, in virtù del criterio della radice. Se l > 1, dalla medesima definizione:

È istruttivo l'esempio di fig. 1.

Tags: criterio della radice, serie assolutamente convergente