Moto di una barra vincolata a una corda
Settembre 22nd, 2021 | by Marcello Colozzo |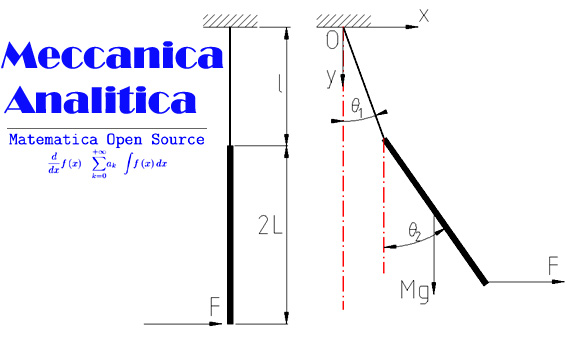
Esercizio
Una corda senza massa, lunga l e fissata ad un soffitto, sostiene una barra sottile di massa M, lunga 2L, alla cui estremità libera è applicata una forza orizzontale F (fig. 1). Scrivere le equazioni di Lagrange per tale sistema. Per tempi molto brevi - ragion per cui gli angoli sono piccoli - determinare gli angoli formati da corda e barra.
Considerando lo stato di riposo al tempo t=0, disegnare il sistema per illustrare il moto iniziale della barra.
Soluzione
Come è evidente dalla fig. 1 il moto si sviluppa e rimane in un piano verticale. Il baricentro della barra ha le seguenti coordinate cartesiane:
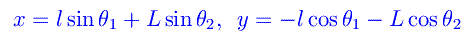
Le componenti della velocità sono:
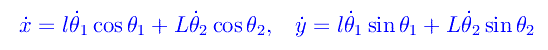
e il momento di inerzia della barra rispetto all'asse perpendicolare baricentrico vale:

Dunque l'energia cinetica della barra è
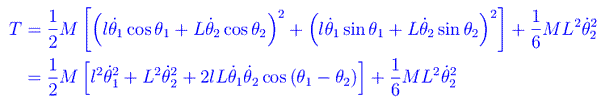
e la sua energia potenziale gravitazionale:

Per definizione, il potenziale della forza è
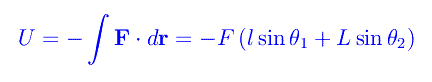
Quindi la lagrangiana:

e le equazioni di Lagrange saranno:
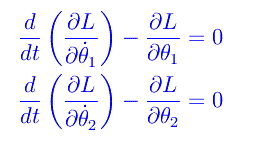
Calcoliamo le derivate parziali e otteniamo:

Notiamo che se F è piccola lo sono pure le 4 variabili, quindi le equazioni appena scritte si possono semplificare in
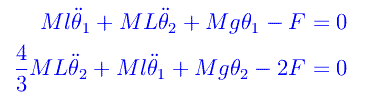
Il moto inizia con il sistema a riposo a t=0. Dopo, per un tempo molto breve Δt, la forza può considerarsi di tipo impulsivo FΔt, e così pure il momento torcente FLΔt rispetto al baricentro.

Dunque concludiamo

come illustrato in figura:
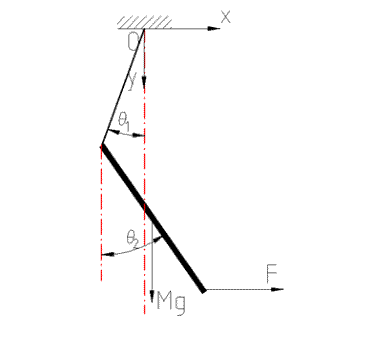
Tags: barra, corda, lagrangiana, moto
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











