Ortogonalizzazione di Schmidt
Maggio 14th, 2021 | by Marcello Colozzo |
Teorema
Ogni spazio unitario ammette basi ortonormali
Dim.
Sia {ei} una qualunque base non ortonormale di uno spazio unitario V. Costruiamo una nuova base {fi}} attraverso il seguente procedimento:
Sviluppando il determinante:
Dalla definizione di f2 segue
Sviluppando il determinante si perviene:
Per k=3,...,n
Si ha:
No TweetBacks yet. (Be the first to Tweet this post)
Tags: base ortonormale, Ortogonalizzazione di Schmidt, spazio unitario
Articoli correlati
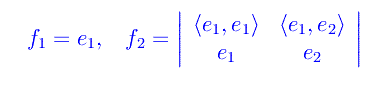
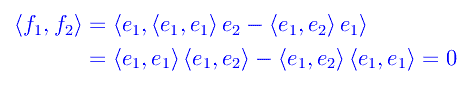
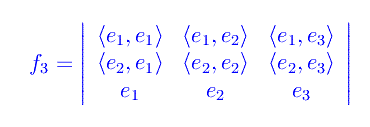
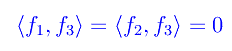
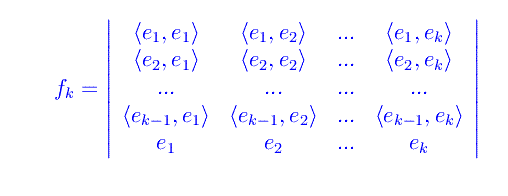
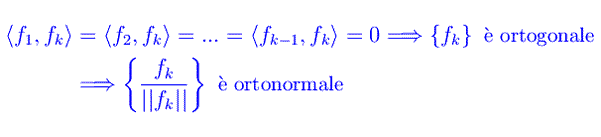


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











