» Esercizi svolti di Matematica e Fisica

Spazi vettoriali unitari. Prodotto interno (o prodotto hermitiano)

Definizione
Uno spazio unitario è uno spazio vettoriale sul campo complesso in cui è definito un prodotto interno (denominato anche prodotto scalare o prodotto hermitiano), cioè un'applicazione

che verifica i seguenti assiomi:

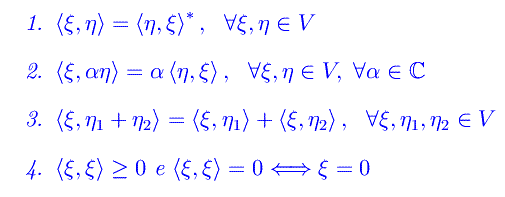
Da tali assiomi segue che la predetta applicazione è bilineare. In analogia con la nozione di "lunghezza" di un vettore di uno spazio vettoriale euclideo, definiamo la norma:

Anche la nozione di ortogonalità si estende facilmente dall'euclideo a un qualunque spazio unitario:

Da ciò segue che tra tutti gli spazi vettoriali, gli spazi unitari sono quelli più "simili" agli spazi euclidei. Vediamo alcuni esempi immediati. Rammentiamo che Cⁿ è uno spazio vettoriale sul campo complesso (non appena introduciamo le operazioni di addizione di vettori e di moltiplicazione di uno scalare per un vettore, con relativi assiomi), i cui elementi sono le n-ple ordinate di numeri complessi. Quindi:

In tal modo Cⁿ assume la struttura di spazio unitario. Vediamo quest'esempio: sia P_n lo spazio vettoriale sul campo complesso, i cui elementi sono i polinomi nell'indeterminata reale x, di grado non superiore ad n. Quindi definiamo:

Tags: prodotto hermitiano, prodotto interno, spazi vettoriali unitari