» Esercizi svolti di Matematica e Fisica

La pandemia da covid quale soluzione di un sistema di equazioni differenziali di cui una stocastica

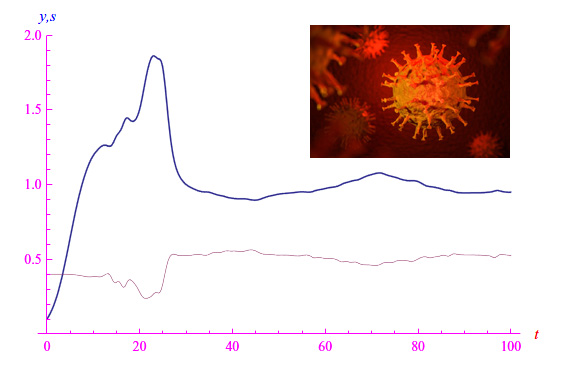
Scriviamo

dove la funzione y(t) modellizza una qualunque pandemia «normalizzata», nel senso che il valore di Plateau è posto pari a 1. Il coefficiente r > 0 è il tasso di contagio (non quello «efficace», ossia il famigerato Rt 🙂 ), mentre la grandezza s(t) denota l'azione di smorzamento/contenimento i.e. un qualunque lockdown o una terapia medica. La novità di questo modello è che s non è un parametro, bensì una soluzione di un'equazione differenziale stocastica. Precisamente la seconda, ove w denota un white noise. Quest'ultimo è facilmente implementabile nell'ambiente di calcolo Mathematica, per cui possiamo provare ad integrare il predetto sistema assumendo r=1.5, mentre le condizioni iniziali del corrispondente problema di Cauchy sono

Si ricordi che y(t) è una popolazione normalizzata, quindi non deve sorprendere il valore iniziale assegnato. Integrando numericamente il sistema, otteniamo gli andamenti plottati in fig. 1, mentre in fig.

Tags: covid, equazioni differenziali stocastiche, pandemia