Curve integrali di un campo vettoriale

Novembre 15th, 2020 | by Marcello Colozzo |

curve integrali di un campo vettoriale,equazioni differenziali

Il sistema di equazioni differenziali (scritto in precedenza è un caso particolare di:

dove X(t,x,y) e Y(t,x,y) sono funzioni reali assegnate definite in un aperto A di R³, ivi continue e lipchitziane nelle variabili x,y. Il sistema può essere scritto a sua volta scritto in forma vettoriale:


essendo


Definizione
Se x(t) è un integrale del sistema, la curva di rappresentazione parametrica

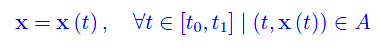
si dice curva integrale del campo vettoriale V(t,x). Cioè

Scarica un esercizio svolto

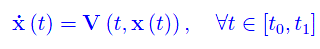
No TweetBacks yet. (Be the first to Tweet this post)

Tags: ,

Articoli correlati

Commenta l'esercizio