Area di una figura piana (integrali doppi)
Maggio 30th, 2020 | by Marcello Colozzo |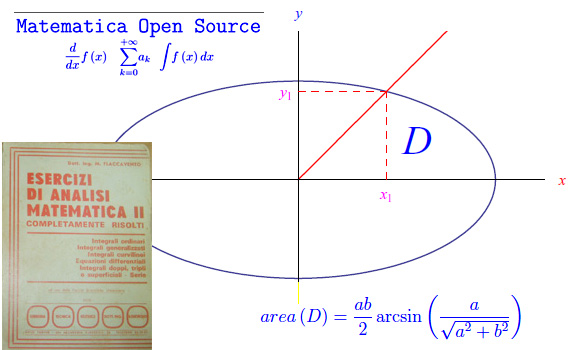
Esercizio n.7, pag. 235 del Flaccavento che comunque riporta un risultato errato. (Abbiamo controllato con Mathematica).
Calcolare l'area della regione del piano limitata dal semiasse positivo delle x, dall'ellisse di semiassi a e b e dalla retta di equazione x=y (fig. 1).
Soluzione
Determiniamo innanzitutto le coordinate cartesiane del punto di intersezione della retta o meglio della semiretta x=y (per y>0) e dell'ellisse:
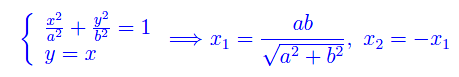
La seconda radice non ci interessa, per cui la scartiamo. L'ordinata del punto di intersezione è ovviamente y1=x1. L'area richiesta altro non è che la misura del dominio di fig. 1 che si potrebbe partizionare in due domini normali rispetto all'asse x. In realtà tale dominio è normale anche rispetto all'asse y. Infatti, se nell'equazione dell'ellisse esprimiamo la variabile x in funzione di y, si ha:
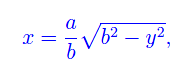
per cui guardando la figura si ottiene
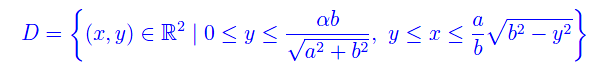
Quindi
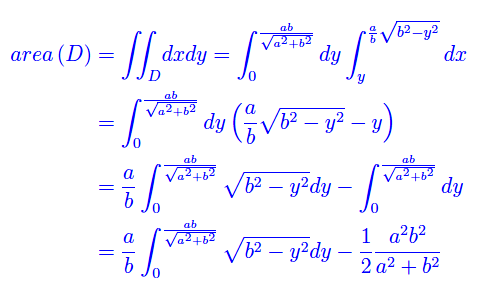
Calcoliamo a parte l'integrale rimasto inespresso a secondo membro dell'equazione appena scritta. Riferiamoci all'integrale indefinito, eseguendo un'integrazione per parti:
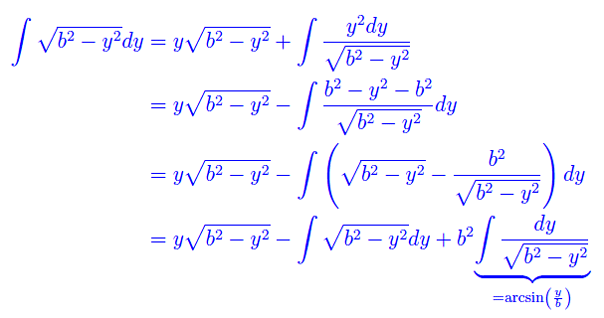
Cioè
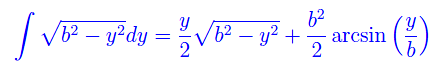
Ne segue
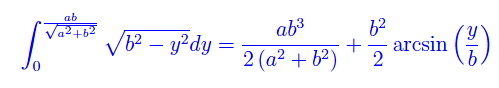
che sostituita nell'equazione più sopra, restituisce il risultato riportato in fig. 1.
No TweetBacks yet. (Be the first to Tweet this post)
Articoli correlati



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











