Incertezza sulla posizione di una particella la funzione d'onda è un pacchetto d'onde
Maggio 13th, 2020 | by Marcello Colozzo |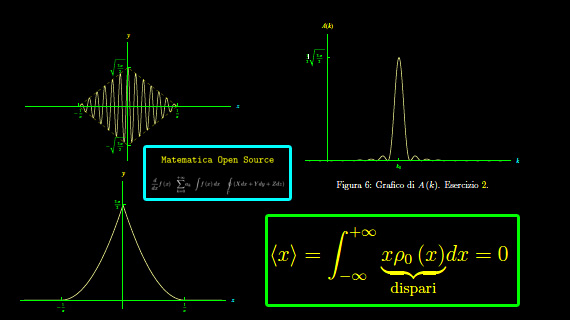
Continuiamo l'esercizio di ieri.
Per calcolare la deviazione quadratica media Δx, dobbiamo dapprima calcolare i valori medi
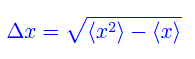
avendosi
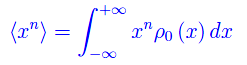
essendo ρ0(x)=|ψ0(x)|² la densità di probabilità di trovare la particella in un assegnato intervallo infinitesimo [x,x+dx]. Abbiamo, dunque
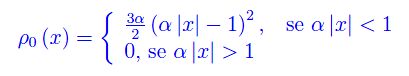
che può essere prolungata per continuità in x=±1/a, avendosi ρ0(±1/a)=0. La funzione ρ0(x) è manifestamente pari e il suo grafico in [-1/a,1/a] è l'unione di due archi di parabola aventi vertici in (±1/a,0) rispettivamente. Ad occhio vediamo che
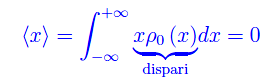
Calcoliamo
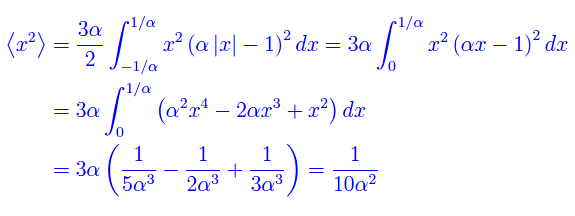
Ne segue
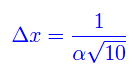
No TweetBacks yet. (Be the first to Tweet this post)
Tags: indeterminazione, pacchetto d'onde, particella, posizione
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











