[¯|¯] Cambiamento di base. Criterio di tensorialità
Marzo 8th, 2020 | by Marcello Colozzo |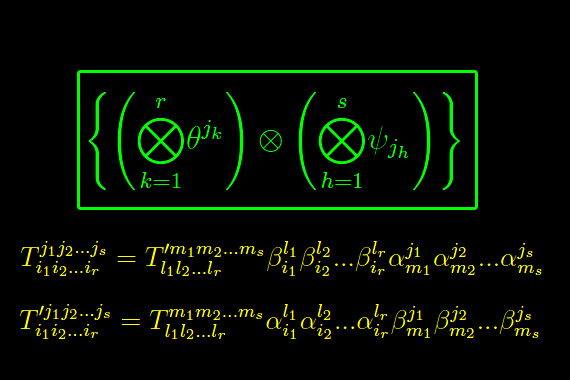
Per quanto visto in precedenza, comunque prendiamo uno spazio vettoriale finito-dimensionale (su un campo K), è univocamente definito lo spazio vettoriale
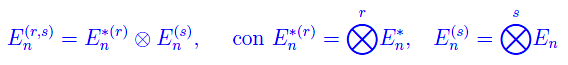
i cui elementi sono i tensori misti di rango r+s. Ci proponiamo di stabilire la legge di trasformazione di tali enti in seguito a un cambiamento di base nel predetto spazio. A tale scopo, osserviamo innanzitutto che un cambiamento di base nello spazio vettoriale, per così dire, di partenza ossia E_{n}, induce un cambiamento di base nel duale e nel biduale e quindi, in En(r,s). Infatti, assegnare una base in En equivale ad assegnare una base nel duale e nel biduale (ove quest'ultimo si identifica con E<n a meno di un isomorfismo naturale). In simboli:
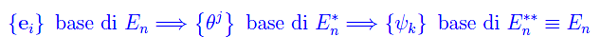
Ora non dobbiamo fare altro che scrivere le leggi di trasformazione dei vari vettori di base quando si passa da {ei} a una nuova base {ei'}. Denotando con αij e ßji gli elementi di matrice della matrice di passaggio P (dalla vecchia alla nuova base) e della sua inversa (gli indici in alto sono indici di riga), si ha:
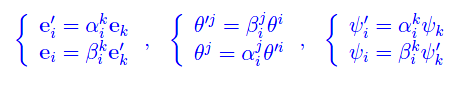
Ritornando nello spazio vettoriale En(r,s), dove una base è
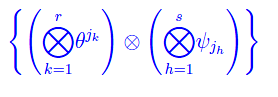
si ha
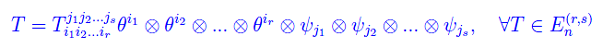
In seguito al predetto cambiamento di base il medesimo tensore si scrive:
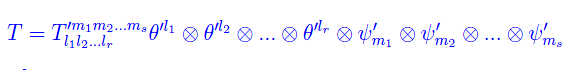
Per quanto precede
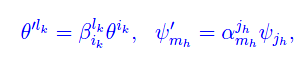
onde
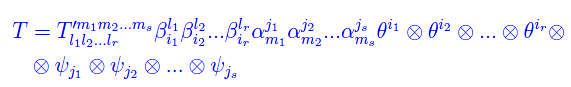
che confrontata con l'eq. scritta più sopra
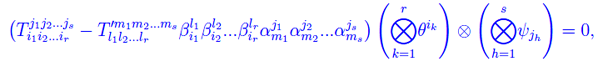
dove a secondo membro troviamo il vettore nullo di En(r,s). Segue
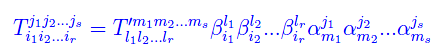
Viceversa, possiamo scrivere il tensore T come combinazione lineare dei nuovi vettori di base:
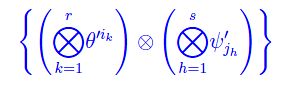
Precisamente:
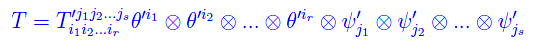
mentre nella vecchia base:
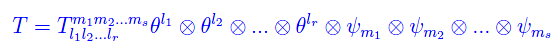
I vettori di base trasformano come
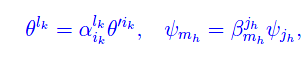
per cui
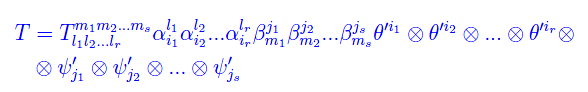
che confrontata con l'eq. scritta più sopra
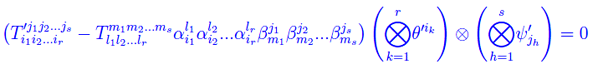
Cioè
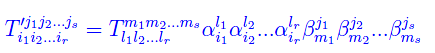
Le formule trovate esprimono il modo di trasformarsi di un tensore quando si passa da una base all'altra di En(r,s). Più precisamente, sussiste il seguente
Criterio di tensorialità
Affinché un sistema di nr+s grandezze
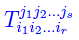
riferite a una base
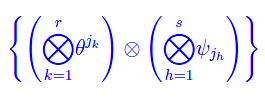
possa essere considerato come il sistema delle componenti di un tensore r-covariante e s-covariante, occorre e basta che il predetto sistema si trasformi secondo la legge seguente:
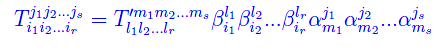
o ciò che è lo stesso:
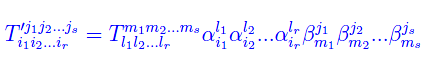



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











