[¯|¯] Tensori covarianti di rango r

Febbraio 27th, 2020 | by Marcello Colozzo |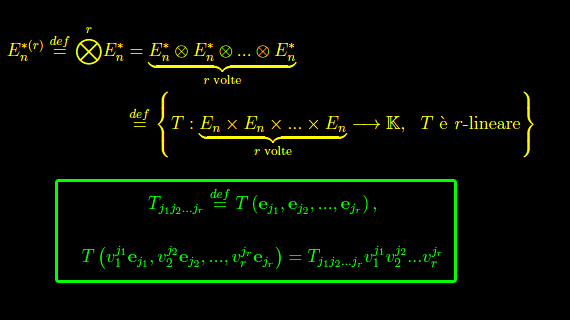

equazione di continuità,bilancio,coronavirus,teorema della divergenza

Dopo aver introdotto i tensori di rango 2 (covarianti, controvarianti, misti), dobbiamo generalizzare tali definizioni passando ai tensori di rango r. Per ora ci riferiamo ai tensori covarianti; la generalizzazione è molto semplice: siamo partiti dalle 0-forme (scalari), passando alle 1-forme (forme lineari o vettori covarianti) e quindi, alle 2-forme (forme bilineari o tensori covarianti di rango 2). Ne consegue che un tensore covariante di rango r altro non è che una r-forma, ossia una forma multilineare (= lineare rispetto ai singoli argomenti che esprime la sua espressione analitica):

Scarica la lezione in pdf

No TweetBacks yet. (Be the first to Tweet this post)