[¯|¯] Curve che si intrecciano ed iniettività locale
Febbraio 19th, 2020 | by Marcello Colozzo |
Secondo alcuni Autori, una curva regolare è priva di punti multipli. Nell'approccio che invece stiamo seguendo, abbiamo rilassato tale condizione richiedendo però, il non annullarsi simultaneo delle derivate delle funzioni componenti della rappresentazione parametrica assegnata, affinché quest'ultima sia regolare. Per quanto visto, tale condizione garantisce l'iniettività locale della funzione vettoriale che implementa la predetta rappresentazione, ma non esclude la presenza di punti multipli, giacché l'iniettività locale non implica quella globale. La fig. 1 mostra l'esempio di una curva piana con un punto doppio.
Precisamente, se la funzione vettoriale
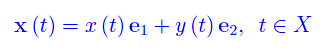
definisce una rappresentazione parametrica della curva in questione, si ha:

giacchè la curva ha un punto doppio. Dall'andamento vediamo che sia l'ascissa sia l'ordinata inizialmente sono funzioni crescenti di t, per poi raggiungere un massimo relativo, e quindi divenire funzioni decrescenti. Tuttavia, ci si aspetta (salvo casi particolari) che i massimi relativi vengono raggiunti per diversi valori del parametro, come vediamo in fig. 1.

Nel caso contrario, le derivate si annullerebbero simultaneamente e la rappresentazione sarebbe non regolare. Quindi per t0 diverso da t0', la funzione vettoriale x(t) conserva l'iniettività locale anche intorno ai predetti punti. Infatti:
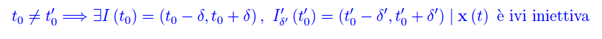



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











