» Esercizi svolti di Matematica e Fisica

[¯|¯] Accelerazione radiale e accelerazione trasversale

Gennaio 7th, 2020 | by Marcello Colozzo |

In una precedente lezione abbiamo visto che in un moto piano il vettore accelerazione ammette la seguente decomposizione

Rammentiamo velocemente che i vettori componenti sono rispettivamente l'accelerazione tangenziale e l'accelerazione normale. Con ovvio significato dei simboli:

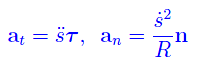
con il raggio di curvatura R dato da

Abbiamo poi visto) che in un moto piano il vettore velocità ammette la seguente decomposizione rispetto a un sistema di coordinate polari (r,φ):

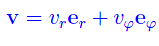
essendo e_r,e_φ una coppia di versori ortogonali, di cui il primo parallelo al vettore posizione r, mentre

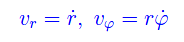
sono rispettivamente la velocità radiale e la velocità trasversale. Ciò premesso, decomponiamo il vettore accelerazione nelle componenti radiale e trasversale:

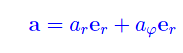
come in fig. 1. A tale scopo ricordiamo che:

da sostituire nella rappresentazione cartesiana del predetto vettore:

a patto di calcolare le derivate seconde rispetto al tempo, delle funzioni

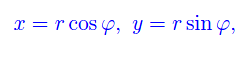
ottenendo

Sviluppando e semplificando:

onde

Tags: accelerazione radiale, accelerazione trasversale

Articoli correlati