[¯|¯] Esercizio 2 svolto sul moto piano in coordinate polari |

[¯|¯] Esercizio 2 svolto sul moto piano in coordinate polari

Dicembre 21st, 2019 | by Marcello Colozzo |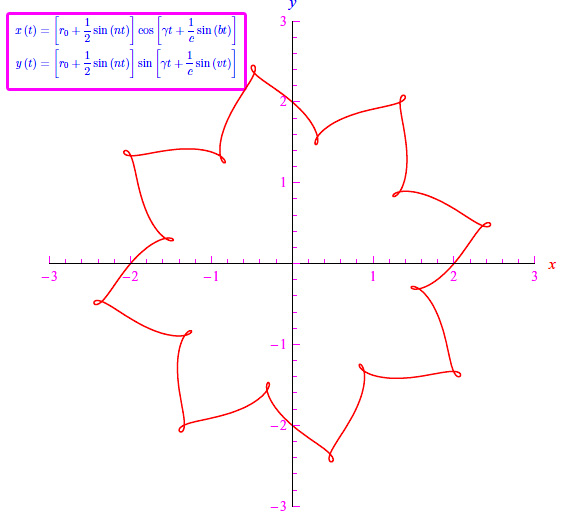

moto piano,coordinate polari,velocità radiale, velocità trasversale — **Fig. 1**

Esercizio

Studiare il seguente moto piano in coordinate polari:

dove n è un intero naturale non nullo con le dimensioni dell'inverso di un tempo, mentre γ > 0 è una costante con le dimensioni dell'inverso di un tempo. Quale è il minimo valore di r₀?

Soluzione
Vediamo innanzitutto che deve essere r(t) >= 0, per cui

Osservando che sin(nt)> = -1, si ha r₀ > = 1/2. Tale grandezza è il valore iniziale (a t=0) del raggio vettore. Ne consegue che il raggio vettore del punto materiale oscilla sinusoidalmente tra r₀-1/2 e r₀+1/2. L'anomalia φ invece, oscilla sinusoidalmente intorno alla retta di coefficiente angolare γ. Passando alle coordinate cartesiane, otteniamo la seguente rappresentazione parametrica della traiettoria: