[¯|¯] Da un problema ai limiti a un problema di Cauchy

Settembre 23rd, 2019 | by Marcello Colozzo |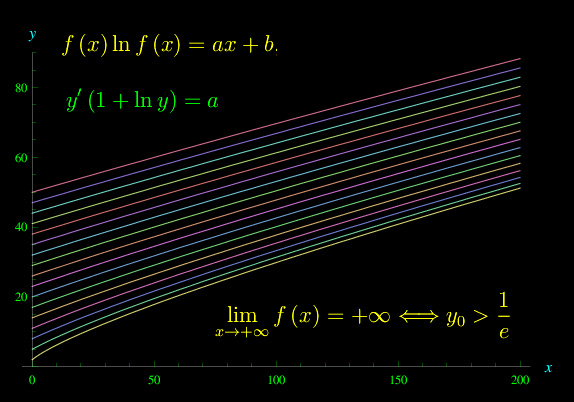

integrale generale,problema ai limiti,problema di cauchy — **Fig. 1**

Un utente del nostro gruppo, ha proposto il problema funzionale illustrato in fig. 1. Accanto alle soluzioni proposte da altri due utenti (la prima è in questo pdf. La seconda, invece, invoca la funzione W di Lambert), proponiamo una soluzione basata sulle equazioni differenziali.

Più specificatamente, è facile verificare che l'equazione funzionale proposta altro non è che un integrale particolare di un'equazione differenziale del primo ordine non lineare. L'integrale particolare è univocamente determinato da una condizione ai limiti (divergenza all'infinito). Siccome è più facile risolvere un problema di Caucy, nella soluzione proposta viene esaminato un algoritmo che permette di trovare la soluzione per via numerica con un'assegnata condizione iniziale

Scarica la soluzione in pdf.

No TweetBacks yet. (Be the first to Tweet this post)