» Esercizi svolti di Matematica e Fisica

[¯|¯] Enumerando gli zeri della funzione zeta di Riemann

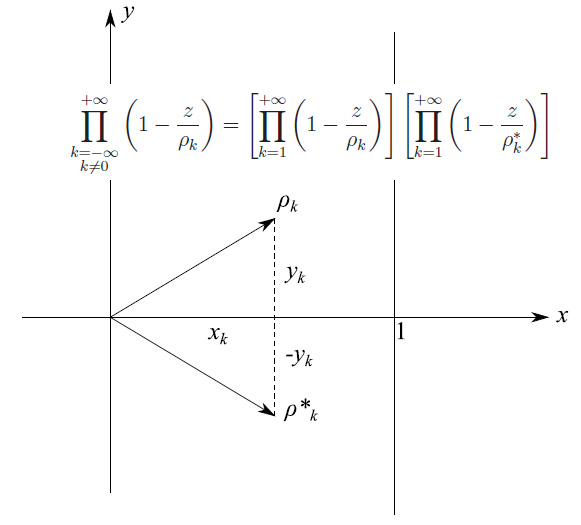
Scopo di questo handbook è l'enumerazione degli zeri della funzione zeta di Riemann, sfruttando la nota proprietà della funzione &xi (di Riemann), e cioè tali funzioni hanno in comune gli zeri non banali. Da alcune considerazioni basate sulla simmetria rispetto all'asse reale e alla retta critica, esibita dalla ξ si ha che il noto sviluppo di Hadamard si esprime attraverso un prodotto infinito bilaterale. È interessante studiare la convergenza di tale prodotto.

Scarica il file in formato pdf

Tags: funzione Zeta di Riemann, zeri non banali