[¯|¯] Quando la somma non è una somma diretta
Luglio 1st, 2017 | by Marcello Colozzo |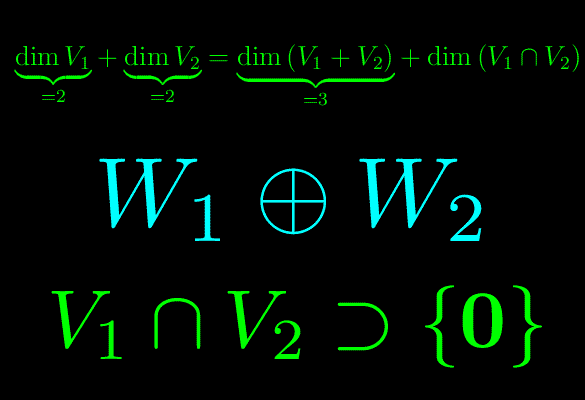
Esercizio
Nello spazio vettoriale R³ si considerino i seguenti sottospazi:
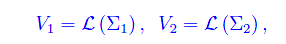
dove
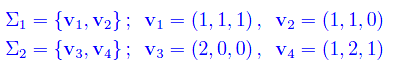
Determinare una base della somma e dell'intersezione dei predetti sottospazi.
Soluzione
Il sistema di vettori Σ1 è linearmente indipendente, per cui è una base di V1 => dim(V1)=2 Allo stesso modo dim(V2)=2, giacché Σ2 è linearmente indipendente. Riesce

D'altra parte
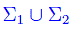
è lineramente dipendente, giacché
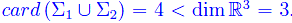
Per determinare una base della somma V1+V2 procediamo per trasformazioni elementari

Sostienici
No TweetBacks yet. (Be the first to Tweet this post)
Tags: intersezione, somma, somma diretta, sottospazio, sottospazio vettoriale
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











