» Esercizi svolti di Matematica e Fisica

[¯|¯] L'equazione del bilancio e l'equazione di continuità

Maggio 18th, 2017 | by Marcello Colozzo |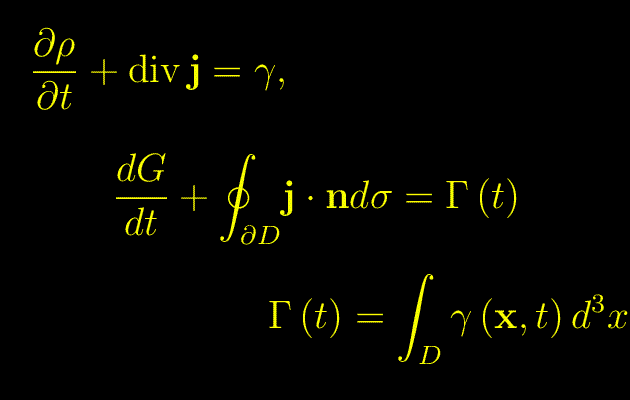

Sia G(t) una grandezza scalare di densità ρ(x,t):

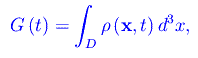
per un assegnato dominio D di R³. Dal momento che ρ(x,t) è una funzione delle coordinate (x,y,z) e del tempo t, possiamo immaginare che essa venga "trasportata". Definiamo allora un campo vettoriale j(x,t) - denominato densità di corrente di G(t) - tale che se ds è un qualunque elemento di superficie e n il versore normale, j(x,t)·nds è la quantità di grandezza che attraversa ds nell'unità di tempo. Ciò implica che

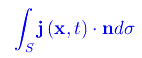
è la quantità di grandezza che attraversa la superficie S nell'unità di tempo. Dimostriamo il seguente teorema:

Teorema
L'equazione del bilancio per la grandezza G(t) di densità ρ(x,t) e densità di corrente j(x,t) è

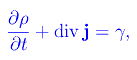
dove γ(x,t) è la densità di velocità di creazione/distruzione della grandezza G(t):

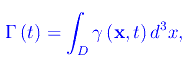
essendo Γ(t) la velocità di creazione/distruzione di G(t).

Scarica la dimostrazione in formato pdf

Tags: equazione del bilancio, equazione di continuità, teorema della divergenza

Articoli correlati