[¯|¯] Applicazioni continue
Aprile 2nd, 2017 | by Marcello Colozzo |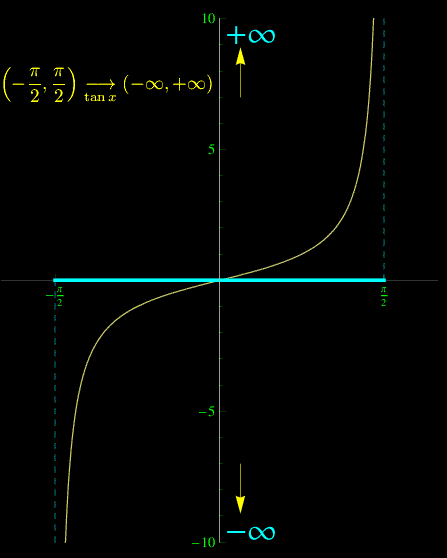
Fig. 1
Nella lezione. abbiamo introdotto la nozione di omeomorfismo nel caso euclideo, riferendoci in particolare a R¹ attraverso l'esempio della funzione tan(x) che risulta essere un omeomorfismo tra l'aperto (-π/2,π/2) e R¹ medesimo (vedasi fig. 1). Tuttavia, per rendere operativa la definizione di varietà topologica dobbiamo estendere la definizione di omeomorfismo tra aperti di punti di uno spazio di Hausdorff e aperti di Rn. A tale scopo rammentiamo che un omeomorfismo è un'applicazione continua e iniettiva e suriettiva con inversa continua. Quindi, il primo passo consiste nell'estendere la nozione di continuità da Rn a un qualunque spazio topologico (S,Θ). Come è ben noto, nel caso euclideo un'applicazione
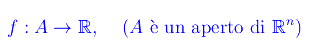
si dice continua in un punto P0 di A se
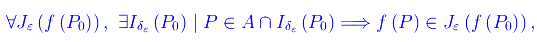
dove
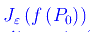
denota un intorno di f(P0) di raggio ε, mentre
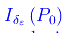
indica un intorno di P0 di raggio δε. Passiamo ora a un'applicazione tra due spazi topologici (S,Θ) e (S',Θ'). Precisamente, diremo che l'applicazione
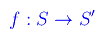
è continua in un punto p0 di S se
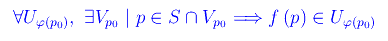
Se f risulta continua in ogni punto di S, diremo che f è ivi continua. Si noti come abbiamo utilizzato la "notazione topologica" per denominare i rispettivi intorni. La definizione appena vista diviene identica a quella precedente se S è un sottoinsieme di Rn e S'=R, assumendo come topologia per i rispettivi spazi, la topologia euclidea. Siamo ora in grado di definire:
Definizione
Assegnati gli spazi topologici (S,Θ) e (S',Θ'), l'applicazione
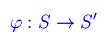
è un omeomorfismo se è iniettiva, suriettiva e continua, insieme all'inversa φ-1.



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











