[¯|¯] Applicando il principio di sostituzione degli infiniti
Marzo 9th, 2017 | by Marcello Colozzo |
Calcolare questo limite applicando il Principio di sostituzione degli infiniti.
Soluzione
Il rapporto si presenta nella forma indeterminata oo/oo. A numeratore abbiamo x² che è un infinito del secondo ordine rispetto all'infinito di riferimento u(x)=x. Determiniamo l'ordine di infinito xarctan(x)
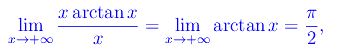
per cui xarctan(x) è del primo ordine e come tale trascurabile rispetto a x². L'altro addendo sin x è non regolare per x->+oo, ma è limitato, cosicché possiamo trascurararlo.
Passiamo a denominatore. Qui vediamo che
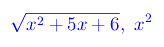
sono manifestamente infiniti del secondo ordine, per cui possiamo trascurare l'addendo -3x. Possiamo poi svincolarci dalla radice osservando che
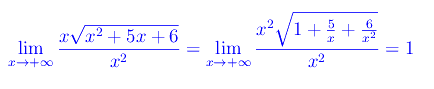
Cioè
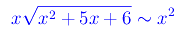
In definitiva il limite proposto diventa:
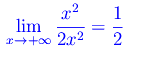
No TweetBacks yet. (Be the first to Tweet this post)
Tags: infiniti, limiti, principio di sostituzione degli infiniti
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











