[¯|¯] Infinitesimo [infinito] di riferimento
Febbraio 23rd, 2017 | by Marcello Colozzo |
Per poter quantificare il concetto di ordine di un infinitesimo (o di un infinito) è necessario definire un infinitesimo (o un infinito) di riferimento. Per fissare le idee, iniziamo con gli infinitesimi. Nella classe I(x0) di tutti e soli gli infinitesimi in x0, scegliamo ad arbitrio un infinitesimo di riferimento (o infinitesimo campione) u(x). La scelta più semplice è
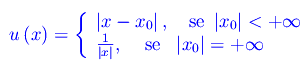
Osserviamo che comunque prendiamo α>0, riesce:
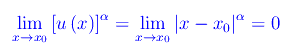
Cioè
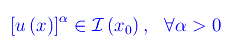
Inoltre, per ogni ß>0
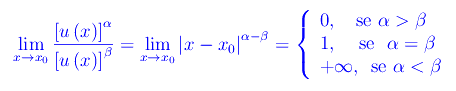
In altri termini, se α>ß l'infinitesimo [u(x)]α è di ordine superiore a [u(x)]ß, e viceversa se α<ß. Se α=ß gli infinitesimi [u(x)]α e [u(x)]ß sono equivalenti. Ne consegue:
Definizione 1
Il numero reale α>0 si dice ordine dell'infinitesimo [u(x)]α.
Ciò premesso, sussiste la seguente definizione:
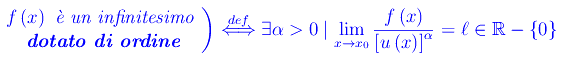
Il numero reale α>0 si dice ordine di f(x) rispetto all'infinitesimo di riferimento u(x).
In maniera del tutto analoga si definisce l'ordine di un infinito f(x) della classe J(x0). Più precisamente, se u(x) è l'infinitesimo di riferimento nella classe I(x0), si assume come infinito di riferimento nella classe J(x0), l'infinito:
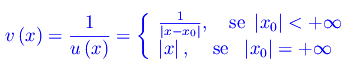
Naturalmente:
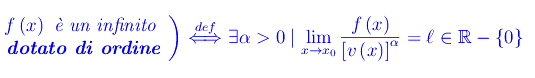
Il numero reale α>0 si dice ordine di f(x) rispetto all'infinito di riferimento v(x).
No TweetBacks yet. (Be the first to Tweet this post)
Tags: infinitesimi, infinitesimo di riferimento, infiniti, infinito di riferimento
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











