[¯|¯] Saltando con dolcezza

Gennaio 13th, 2017 | by Marcello Colozzo |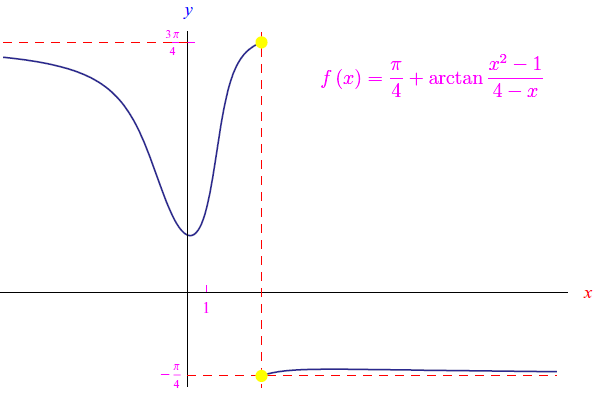

limiti,funzioni circolari inverse,arcotangente,discontinuità di prima specie

Fig. 1

Determinare il comportamento della funzione illustrata in fig. 1, agli estremi del suo campo di esistenza.

Soluzione
La funzione è definita in

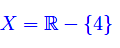
limiti,funzioni circolari inverse,arcotangente,discontinuità di prima specie

Calcoliamo
limiti,funzioni circolari inverse,arcotangente,discontinuità di prima specie

Ne consegue che x=4 è un punto di discontinuità di prima specie. Calcoliamo

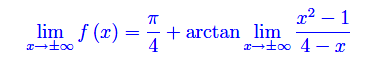
limiti,funzioni circolari inverse,arcotangente,discontinuità di prima specie

Ma

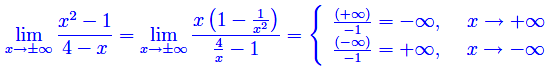
limiti,funzioni circolari inverse,arcotangente,discontinuità di prima specie










Segue
limiti,funzioni circolari inverse,arcotangente,discontinuità di prima specie

Cioè le rette orizzontali

limiti,funzioni circolari inverse,arcotangente,discontinuità di prima specie

sono rispettivamente asintoti orizzontali a destra e a sinistra per il diagramma cartesiano della funzione riportato in fig. 1.








No TweetBacks yet. (Be the first to Tweet this post)

Tags: , , ,

Articoli correlati

Commenta l'esercizio