» Esercizi svolti di Matematica e Fisica

[¯|¯] Esempio di "mostro topologico"

Gennaio 12th, 2017 | by Marcello Colozzo |

---

Esercizio
Classificare i punti di discontinuità della funzione

---

Riguardo al campo di esistenza, dobbiamo imporre

Per x->0 la funzione sin(1/x) è non regolare e tale è la funzione assegnata, per cui

Studiamo il comportamento negli infiniti punti

Determiniamo preliminarmente i limiti

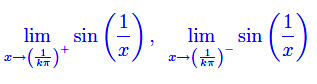
Abbiamo

Ne consegue

k pari:

k dispari

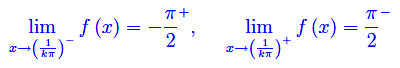
Quindi i punti x_k sono di discontinuità di prima specie per f, con salto

Definiamo

Cioè S è l'insieme dei punti di discontinuità della funzione. Dal momento che x=0 è punto di accumulazione per S, si ha che in ogni intorno di x=0 di ampiezza comunque piccola, cadono infiniti punti di S, i.e. punti di discontinuità per f, come illustrato nel grafico di fig. 1.

Tags: discontinuità di prima specie, infiniti punti di discontinuità, limiti, topologia

Articoli correlati