[¯|¯] Ascissa curvilinea sul grafico di una funzione reale di una variabile reale
Novembre 13th, 2016 | by Marcello Colozzo |
Fig. 1. Grafico della funzione assegnata
Assegnata la funzione:
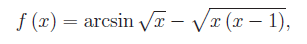
stabilire un sistema di ascisse curvilinee (Os), dove O(0,0) è l'origine del riferimento cartesiano R(Oxy), sulla curva y=f(x), orientando la curva nel verso delle x crescenti. Si determini, infine, la rappresentazione naturale della curva assegnata.
Soluzione
Determiniamo innanzitutto ilcampo di esistenza X della funzione assegnata. Deve essere:
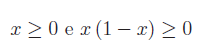
La prima è banale, la seconda immediata. Quindi è X=[0,1].
Senza eseguire uno studio di funzione tracciamo il grafico aiutandoci con Mathematica ottenendo il plot di fig. 1
No TweetBacks yet. (Be the first to Tweet this post)
Tags: ascissa curvilinea, equazioni parametriche, grafico funzione, lunghezza arco di curva
Articoli correlati
Congettura di Riemann
Trasformata discreta di Fourier
Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier 
Infinitesimi ed infiniti
Limiti notevoli
Punti di discontinuità
Misura di Peano Jordan
Eserciziario sugli integrali
Differenziabilità 
Differenziabilità (2)
Esercizi sui limiti
Appunti sulle derivate
Studio della funzione
Esercizi sugli integrali indefiniti
Algebra lineare
Analisi Matematica 2
Analisi funzionale
Entanglement quantistico
Spazio complesso
Biliardo di Novikov
Intro alla Meccanica quantistica
Entanglement Quantistico
