[¯|¯] Ancora sul teorema di Lagrange applicato alla cinematica del punto materiale
Ottobre 31st, 2016 | by Marcello Colozzo |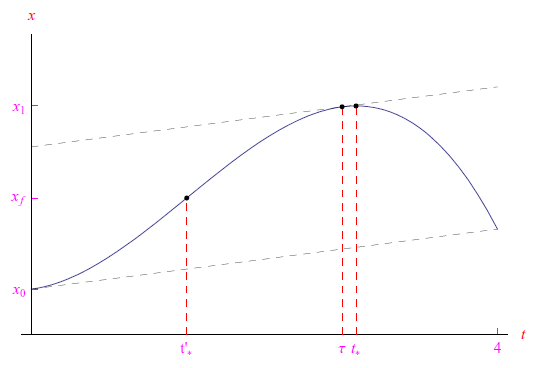
Problema
Nell'intervallo di tempo [0,4s], l'equazione oraria di una particella che si muove su una retta è:
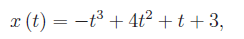
i cui coefficienti a secondo membro hanno le appropriate unità di misura, in modo da esprimere x in metri e t in secondi. Si esegua uno studio di funzione della x(t), determinando poi l'istante in cui la velocità v(t) uguaglia la velocità media nell'intervallo [0,4s]. (Suggerimento: si utilizzi il teorema di Lagrange).
Soluzione
Intersezione con gli assi coordinati t,x
Per l'intersezione con l'asse t dobbiamo risolvere l'equazione
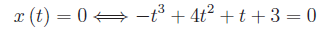
Con l'ausilio di Mathematica vediamo che tale equazione è priva di radici in [0,4]. Inoltre risulta
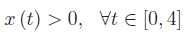
No TweetBacks yet. (Be the first to Tweet this post)
Tags: accelerazione, Calcolo differenziale, Cinematica, teorema di lagrange, velocità
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











