[¯|¯] Ancora sulla non sommabilità di una funzione (sia pur integrabile)

Ottobre 20th, 2016 | by Marcello Colozzo |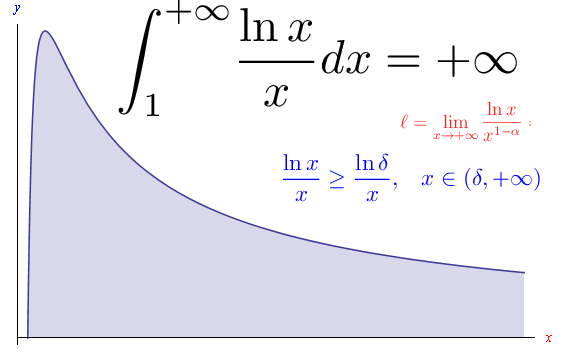

L'esercizio di oggi riguarda la funzione dell'esercizio precedente. Precisamente, si tratta di stabilire la sommabilità di f(x)=ln(x)/x nell'intervallo illimitato [1,+oo). La funzione in esame è manifestamente continua nell'intervallo di integrazione.

Ma dal momento che quest'ultimo è illimitato superiormente, si pone il problema dello studio del comportamento della funzione per x->+oo. Risulterà, come vedremo nel file pdf allegato a questo post, che tale funzione è, per x->+oo, un infinitesimo non dotato di ordine, e ciò rende problematico lo studio della convergenza.
Per i dettagli, scarica l'esercizio in formato pdf.

No TweetBacks yet. (Be the first to Tweet this post)