Equazione differenziale di Riccati: analisi delle soluzioni

Aprile 2nd, 2016 | by Marcello Colozzo |

Riprendiamo il problema di Cauchy relativo all'equazione differenziale di Riccati:

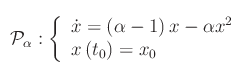
equazione differenziale di riccati,problema di cauchy, popolazione, crescita

Nel file pdf allegato a questo post (vedi in fondo), troviamo l'unica soluzione:

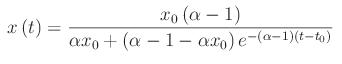
che a tempi brevi è approssimata da una funzione esponenziale:

Inoltre, come è ben noto nella letteratura scientifica, l'equazione di Riccati simula molto bene processi di crescita relativi a una popolazione di insetti. Incidentalmente, l'equazione da cui siamo partiti può essere campionata nel tempo per restituire un'equazione di ricorrenza della famosa mappa logistica.

In questo paradigma, la crescita esponenziale ha una semplice interpretazione: a tempi brevi le risorse dell'ambiente sono praticamente illimitate, dato che ci sono pochi individui nella popolazione. Ma, al progressivo crescere della variabile tempo, nascono nuovi esemplari e ne consegue che le risorse non possono essere più considerate illimitate. Infatti, ora non è più trascurabile il termine -x^2 che tende a frenare la crescita. Ne consegue l'andamento asintotico.

Per ora concludiamo che la crescita esponenziale è un'ottima simulazione per una popolazione batterica, giacchè per questi ultimi le risorse dell'ambiente sono illimitate a tutti i tempi.

Per i dettagli matematici leggi il file pdf

No TweetBacks yet. (Be the first to Tweet this post)