Introduzione alla mappa logistica: l'equazione differenziale di Riccati
Marzo 31st, 2016 | by Marcello Colozzo |
Sia dato un sistema dinamico a tempo continuo
essendo
e a>1 è un parametro. Abbiamo, dunque, il seguente problema di Cauchy:
L'equazione differenziale
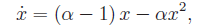
è nota come equazione di Riccati ed è manifestamente non lineare. Può essere resa lineare attraverso il cambio di variabile y=1/x
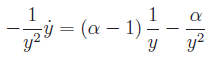
Cioè
Applicando il procedimento standard di integrazione di un'equazione differenziale del primo ordine lineare (calcolo del fattore integrante) si perviene all'integrale generale:
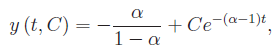
No TweetBacks yet. (Be the first to Tweet this post)
Tags: equazione di riccati, Equazioni differenziali, mappa logistica, Problema di Cauchy
Articoli correlati
Congettura di Riemann
Trasformata discreta di Fourier
Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier 
Infinitesimi ed infiniti
Limiti notevoli
Punti di discontinuità
Misura di Peano Jordan
Eserciziario sugli integrali
Differenziabilità 
Differenziabilità (2)
Esercizi sui limiti
Appunti sulle derivate
Studio della funzione
Esercizi sugli integrali indefiniti
Algebra lineare
Analisi Matematica 2
Analisi funzionale
Entanglement quantistico
Spazio complesso
Biliardo di Novikov
Intro alla Meccanica quantistica
Entanglement Quantistico
