» Esercizi svolti di Matematica e Fisica

Ordine di un infinitesimo e parte principale (con Mathematica)

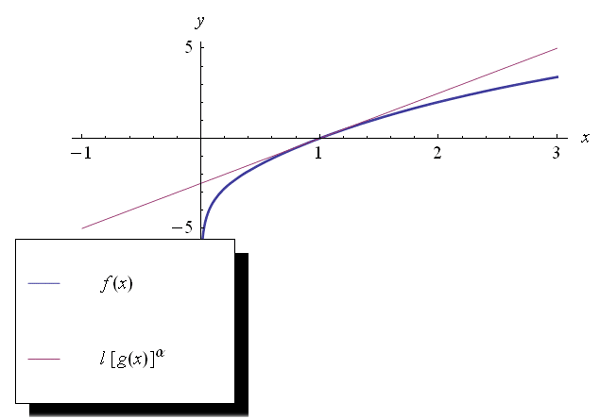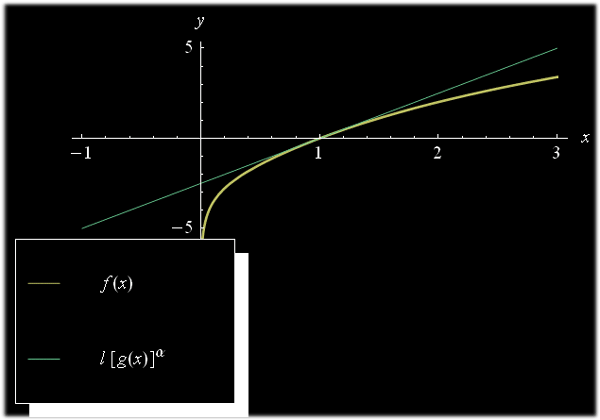
Con Mathematica è possibile scrivere una semplice routine per il calcolo dell'ordine e della parte principale di un infinitesimo.

Dopo aver aperto un notebook, scriviamo:

Si noti l'utilizzo dell'assegnazione ritardata. Nel caso contrario, Mathematica restituisce un messaggio di errore, in quanto (ovviamente!) non riesce a calcolare il limite, non conoscendo le espressioni analitiche delle funzioni e il valore di x0.

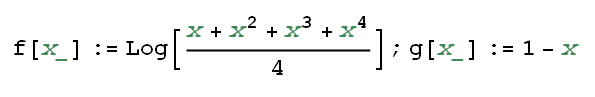
Definiamo:

Ora per vedere per quale valore di alfa il limite è reale e non nullo, utilizziamo il comando Table[]

Cioè alfa=1. Dopo aver rimosso tale variabile, ridichiarandola con valore 1, scriviamo:

essendo p(x) la parte principale. A questo punto è istruttivo confrontare localmente il grafico di f(x) con quello di p(x). A tale scopo scriviamo, dopo aver caricato il pacchetto PlotLegends:

Ad esempio, per delta=2 otteniamo i grafici riportati nella fig. in alto.

Tags: Mathematica, ordine di un infinitesimo, parte principale