» Esercizi svolti di Matematica e Fisica

[¯|¯] La funzione esponenziale nel campo complesso

Negli appunti di oggi trattiamo la funzione esponenziale nel campo complesso (in riferimento alla precedenti lezioni sulle funzioni olomorfe). Il nostro punto di partenza è la dimostrazione della formula:

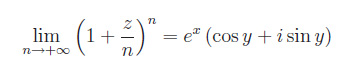
che suggerisce la seguente definizione:

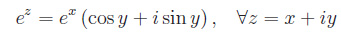
La funzione esponenziale è olomorfa su tutto il piano complesso.

Per dimostrarlo basta applicare il teorema dimostrato nella suddetta lezione, secondo cui condizione necessaria e sufficiente affinchè una funzione complessa sia olomorfa in un campo A, e che essa sia ivi differenziabile secondo Stolz e che soddisfi le equazioni di Cauchy-Riemann (nel campo A).

Scarica gli appunti in formato pdf

Tags: campo complesso, Formula di Eulero, funzione esponenziale