» Esercizi svolti di Matematica e Fisica

[¯|¯] La restrizione è unica, i prolungamenti infiniti

Settembre 21st, 2014 | by extrabyte |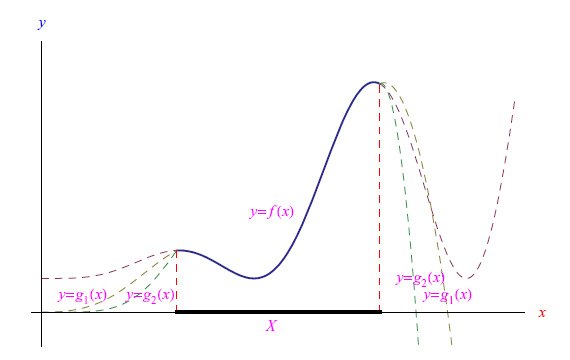

Sia data la funzione reale:

Assegnati due insiemi non vuoti e tali che

consideriamo le funzioni

dove g è tale che

Definizione
f_A si chiama restrizione di f ad A, mentre g si chiama un prolungamento di f su B.

Il grafico di f_A è

dove Γ_f è il grafico di f. Il codominio di f_A è

Per non appesantire la notazione scriviamo f(A). È chiaro che f(A)?f(X). La definizione appena vista è illustrata in figura:

Mentre la restrizione è manifestamente unica, i prolungamenti di f su B contenente X sono infiniti, come illustrato in fig. 1

Ricerca avanzata

• Tutte le categorie Algebra Algebra Lineare Algebra tensoriale Analisi Funzionale Analisi Matematica I Analisi Matematica II Analisi Matematica III Analisi Vettoriale applicazioni degli integrali indefiniti Applicazioni lineari Applicazioni tra insiemi Area di una figura piana Aritmetica Arte e Scienza Asintoti Asintoti di una curva in forma parametrica Astrofisica Autopoiesis Biochimica Biostatistica Calcolo combinatorio Calcolo delle probabilità Calcolo di Limiti Calcolo differenziale Calcolo differenziale – funzioni reali di più variabili Calcolo differenziale – funzioni reali di una variabile Calcolo integrale Calcolo integrale calcolo numerico Calcolo vettoriale Campo di esistenza Campo di esistenza di una funzionre reale di variabile Cinematica del punto Classe di equivalenza Classificazione dei punti di discontinuità CoCoA Composizione di applicazioni Computer science Condizioni di Cebyscev Cosmologia Criteri di regolarità per confronto Crittografia Decomposizione in frazioni semplici Dementia Derive Digital Art Dinamica dei sistemi materiali Dinamica del punto materiale Disequazioni Disequazioni con valore assoluto Disequazioni esponenziali Disequazioni irrazionali Disequazioni logaritmiche Disequazioni razionali Disequazioni razionali intere Disequazioni trigonometriche Editoria Scientifica Editoriale Elettrologia Elettromagnetismo Elettronica Elettronica digitale Elettrotecnica Equazioni differenziali Equazioni differenziali alle derivate parziali Equazioni integrali Fantasticherie cognitive Film Filosofia della Matematica Filosofia della Scienza Fisica atomica Fisica dei giganti Fisica dei superconduttori Fisica del Reattore nucleare Fisica generale 1 Fisica generale 2 Fisica Matematica Fisica nucleare Fisica Tecnica Fisica Teorica formula di Taylor Fortran Funzioni continue Funzioni continue Funzioni di n variabili reali Funzioni di una variabile complessa Funzioni reali di una variabile reale Funzioni sommabili Fusione fredda Geometria Geometria analitica Geometria computazionale Geometria convessa Geometria differenziale Geometria II Geometria III Geometria proiettiva Geometria simplettica GNU Octave GNUPLOT Gravitazione universale Infinitesimi ed infiniti Insieme di definizione Integrale di una funzione reale di n variabili reali Integrale di una funzione reale di una variabile reale Integrali contenenti un trinomio di 2^ grado Integrali curvilinei Integrali definiti Integrali di funzioni iperboliche Integrali di funzioni irrazionali Integrali di funzioni razionali Integrali di superficie Integrali doppi Integrali generalizzati Integrali impropri Integrali indefiniti Integrali trigonometrici Integrali tripli Integrazione di varie funzioni trascendenti Integrazione per decomposizione Integrazione per parti Integrazione per sostituzione Intelligenza Artificiale Introduzione all’analisi matematica LaTeX Le Scienze Libri Limiti di funzioni iperboliche Limiti di funzioni irrazionali Limiti di funzioni reali di più variabili Limiti di funzioni reali di una variabile reale Limiti di funzioni trigonometriche Logica Matematica Maple matematica applicata Matematica discreta Matematica e Arte Matematica finanziaria Matematica&Arte Mathematica Matlab Matrici e determinanti Meccanica analitica Meccanica celeste Meccanica dei corpi rigidi Meccanica dei fluidi Meccanica ondulatoria Meccanica Quantistica Meccanica Quantistica meccanica razionale Meccanica Statistica Meccanica Statistica Metodi matematici della fisica Metodo dei coefficienti indeterminati Metodo di Ostrogradskij Modelli Matematici per l’Ingegneria MuPAD Navigazione Neuroscienze News News&Update Numeri complessi Off Topic Onde in mezzi elastici Pascal Plot Processi d’urto Prodotti infiniti Programmazione Punti di discontinuità QtOctave Quantum Computing Realismo fantastico Relatività Ristretta Relazione di equivalenza Relazioni in un insieme rivista di sintesi scientifica Satelliti Artificiali scientia Scientific Workplace Scienz&Arte Scienza delle Costruzioni Serie Serie di Fourier Serie di Laurent Serie di Taylor Sistemi di disequazioni Sistemi di equazioni lineari Sistemi dinamici Software Soluzioni per via grafica Sostituzione universale di variabile Sostituzioni iperboliche Sostituzioni trigonometriche statistica Storia dell’informatica Storia della Fisica Storia della Matematica Struttura della materia Studio delle funzioni successioni Teoria degli insiemi Teoria dei Giochi Teoria dei Gruppi Teoria dei numeri Teoria dei segnali Teoria dei sistemi dinamici Teoria quantistica dei campi (QFT) Termodinamica topologia Trasformata di Fourier Trasformata di Laplace Trigonometria Umorismo
• Tutti i tag . “fisica del cancro “Probabilità di fuga alle risonanze “resistori in serie [¯|¯] Integrale curvilineo esteso a un arco di parabola cubica 1 elevato a infinito 1-forma 110 e lode 2-sfera 4 maggio 4-vettori controvarianti 5G a beatiful mind A beautiful mind A new kind of Science a relatively stationery U-235 nucleus is bombarded by a 1MeV neutron A remarkable property of the cylindrical helix a U-235 nucleus is bombarded by a neutron Abbondanza di Goldbach accademia dei lincei accelerazione accelerazione complementare accelerazione di coriolis accelerazione di gravità accelerazione di gravità sulla Luna accelerazione media accelerazione normale accelerazione radiale accelerazione tangenziale accelerazione trasversale accelerometro acetilene achille e la tartaruga acido lisergico Actual Sizes of Molecules and Atoms Add new tag addizione adesso adiabatica adroni aereo da caccia aéroglisseur AFT aggiornamento aia Alan Turing Albert Einstein Aldo Ghizzetti Aleph con zero Alexander Grothendieck alfa particle alge Algebra algebra 2 algebra astratta Algebra commutativa Algebra Computazionale algebra di boole Algebra Lineare algebra multilineare algebre di boole algebre di lie algoritmi Algoritmi di clustering algoritmo algoritmo adattivo algoritmo di Elo algoritmo di euclide algoritmo di Fermat Algoritmo di Rabin–Miller algoritmo di strassen algoritmo SOR Alice nel paese dei quanti alien alieni allergie allineamento di punti nel piano allineamento di punti nello spazio allowable change of parameter altezza altezza del livello di un liquido in un tubo altopiano altrove assoluto alzo amazon ambienti amici amici di matematica open source ammortamenti amore analisi analisi asintotica Analisi Complessa Analisi computazionale Analisi Convessa analisi di fourier Analisi Funzionale analisi I Analisi II analisi III analisi matematica analisi matematica 1 analisi matematica 2 Analisi Matematica B Analisi Matematica I Analisi Matematica II Analisi Matematica III Analisi non standard analisi numerica analisi reale analisi spettrale Analisi Vettoriale andrea lo pumo andrea sgarro Andrew Wiles anelli anelli dell’io anello commutativo angolo angolo di sito angolo intersezione Angolo tra due curve angolo tra due vettori anidride carbonica animazione anime dei defunti anisotropie annunci di lavoro anomalia anti-fan anti-telefono tachionico antimmagine antiossidanti antiradar antisymmetric matrix antonino buono antonio de nardis aperti apocalisse apocentro append appiattimento cognitivo Appicazioni geometriche della derivata apple applicazione applicazione antilineare applicazione biiettiva applicazione composta applicazione costante applicazione iniettiva applicazione inversa applicazione lineare applicazione prodotto applicazione suriettiva applicazioni bi-iettive Applicazioni biiettive Applicazioni cinematiche della derivata applicazioni continue applicazioni degli integrali indefiniti applicazioni del differenziale totale Applicazioni della derivata Applicazioni geometriche del differenziale Applicazioni geometriche della derivata Applicazioni iniettive applicazioni lineari applicazioni multilineari applicazioni per android Applicazioni suriettive Applicazioni tra insiemi approssimazione approssimazione di Born-Oppenheimer approssimazione di Riemann approssimazione di stirling approssimazione lineare approssimazione polinomiale approssimazioni appunti appunti di matematica arccos(x) archetipi junghiani archetipo junghiano architettura della complessità arclenghtfactor arco coseno iperbolico arco di circonferenza arco di curva regolare arco di parabola arco seno iperbolico arcoseno arcotangente arcsin arcsinx arctan arctanx area area asteroide area del rettangoloide Area di una figura piana area triangolo aria secca Aritmetica modulare armoniche sferiche array arrayplot Arricchimento dell’uranio 235 per un reattore termico arrotondamento arte arte moderna articoli su altri blog artificio Artificio per risolvere la forma indeterminata 0/0″ artimetica modulare ascensore ascissa ascissa curvilinea asintomatici Asintoti Asintoti del grafico di una funzione Asintoti di una curva asintoti verticali asintoto asintoto obliquo asintoto orizzontale asintoto verticale assegnazione condizionata assegnazione di variabili assegnazione ritardata assi coordinati assiomi asta asteroid asteroide astronave atom Atomic and molecolar structure Atomic and Molecular Structure Atomic and Nuclear Reactions Atomic mass unit atomo atomo di carbonio Atomo di idrogeno Atomo di idrogeno e sistemi idrogenoidi atomo di thomas fermi atomo pesante atterragio attività bio-elettrica del cervello attività fisica attrazione gravitazionale attrito attrito dinamico attrito radente attrito statico attuali positivi attuali postivi attualmente positivi auto-coscienza autofunzione dell’energia autofunzioni autofunzioni dell’energia autoguarigione autoket ortogonali automi cellulari autopoiesi autopoiesis autopubblicazioni autospazio autovalori autovalori e autovettori autovalori reali autovelox autovettori autovettori generalizzati average density of nuclei avogadro’s number avviamento di un reattore nucleare babilonesi bach Bach: un’Eterna Ghirlanda Brillante bacino di attrazione balcone balistica esterna ballerina barbour barcaiolo barcone baricentri baricentro baricentro di un triangolo barra barra metallica barre barriera di potenziale barriera di potenziale parabolica base base biduale base canonica base di jordan base duale base ortonormale base ortonormale rotante base ortornormale baseball basi di lagrange basi ortonormali basket bassetti battaglia navale di Tarawa battimenti baule Be careful to express the normal unit vector as a function of a nonnatural parameter bellezza bersaglio bersaglio mobile bertand russell bidualità biforcazione Biforcazione di Hopf big bang biglia bilancia bilancio biliardo di barry biliardo di novikov binomio di Newton biologia Biostatistica bisettrice BisMag Math Tools black holes blocchi blocco blogs bocca da fuoco bocca della verità bohr born” bottiglia di klein Bourbaki bra braccio di una forza bradioni branduardi brown noise buca di potenziale buca di potenziale unidimensinale buchi neri Buckling di un reattore cacciabombardiere caduta libera calciatore calcio di rigore Calcolatrice grafica Algeo calcolo Calcolo approssimato calcolo combinatorio Calcolo della lunghezza di un arco di curva Calcolo delle probabilità calcolo delle variazioni calcolo di integrali gaussiani Calcolo di Limiti Calcolo differenziale Calcolo differenziale – funzioni reali di più variabili Calcolo differenziale – funzioni reali di una variabile calcolo differenziale assoluto calcolo dimensionale Calcolo integrale calcolo numerico calcolo proposizionale calcolo simbolico calcolo tensoriale calcolo variazionale Calcolo vettoriale Calculation of a limit with the De L’Hospital rule Calculation of the collision density Calculation of the length of an arc of a curve Calculation of the transient component of the neutron flux (nuclear reactor physics) Calculus and limits calculus thomas finney caldaia callisto calore calore di reazione calze di seta cambiamento di base cambiamento di base duale cambiamento di base ortonormale cambio di variabile cammino di integrazione cammino di integrazione chiuso campi campi conservativi campi di forza centrali campi di forza conservativi campi di forza non conservativi campi elettromagnetici campi tensoriali controvarianti campi tensoriali covarianti Campi vettoriali campionamento campo campo a connessione lineare semplice campo centrale campo complesso campo connesso campo conservativo campo dei numeri complessi campo di coscienza Campo di esistenza Campo di esistenza di una funzionre reale di variabile campo di forza centrale campo di forza uniforme campo di forze campo di gravità campo elettrico campo elettromagnetico campo elettrostatico campo gravitazionale campo irrotazionale campo localmente conservativo campo magnetico campo non connesso campo non conservativo campo non-locale campo psi campo radiale campo reale campo scalare campo semplicemente connesso campo solenoidale campo vettoriale canale cancro cane canestro cannone Cantor caos caos deterministico capitoli capodanno caratteri caratteristica tensione-corrente carbon carbonio cariche puntiformi carico carico di rottura carl gustav jung carlo rovelli carrelli carrello carretto carro-attrezzi carrucola carrucola fissa carrucola ideale carrucola mobile carrucole carta locale carte carte da poker carteggio genesis cartella cartesio cartografia CAS casa cashing casi totali caso aperiodico caso critico caso unidimensionale catena catenaria catene di Markov catene di von neumann Cauchy-Riemann causing it to fission cavallo cavallo vapore cavi cavo cavo di traino Ceiling cellular automata cellule tumorali center centro di curvatura centro di massa cerbottana cerchi tangenti cerchio inscritto e allineamenti cerchio osculatore cerebrosoma CERN certificati di primalità certificato di primalità cestista chadwick che cos’è la vita Che t’importa di ciò che dice la gente? chebyschev chiara marletta chop cibernetica ciclo di carnot ciclo di Rankine ciclo teorico cicloide cilindro cilindro parabolico cilindroide Cinematica Cinematica del punto cinematica del punto materiale cinematica monodimensionale cinematica punto materiale cinquina circonferenza circonferenza goniometrica circonferenza trigonometrica circuitazione circuiti elettrici circuito aperto circuito caotico circuito raddrizzatore circuito RC circuito RL circuito RLC cirtuiti elettrici Cissoid of Diocles Cissoide di Diocle Classe di equivalenza classi di equivalenza classical bouncing ball Classificazione dei punti di discontinuità Classificazioni dei punti di discontinuità Cleve Moler climate change cluster cmabio di variabile cobase CoCoA codominio coefficiente angolare Coefficiente angolare della retta tangente coefficiente d’attrito coefficiente di attrito coefficiente di attrito dinamico coefficiente di attrito statico coefficiente di temperatura nucleare coefficiente di trasmissione coefficiente economiche coefficiente economico coefficienti collasso collasso della funzione d’onda collasso funzione d’onda combattimento aereo combinazione lineare di serie combustione come gli hippie hanno salvato la fisica Come io vedo il mondo. La teoria della Relatività complemento algebrico complemento ortogonale complessificazione Complessità computazionale complottismo complottisti componente di un vettore secondo una retta orientata componenti componenti cartesiane componenti controvarianti componenti covarianti componenti di un vettore componenti elettrici componenti elettronici comportamento all’infinito comportamento bioelettrico del cervello Comportamento corpuscolare e ondulatorio della materia Comportamento di una funzione in un intorno di un punto di accumulazione per l’insieme di definizione comportamento magnetico dei superconduttori composizione Composizione di applicazioni composizione di moti armonici composizione rotazioni composizione volumetrica compressione adiabatica computabilità Computation of a limit by comparison of infinities computer computer algebra Computer Algebra System computer quantistici computer quantistico Concavità – convessità – punti di flesso concetto di forza condensatore condivisione dei saperi Condizione di chiusura delle orbite. Commensurabilità con 2 pi greco condizione di complanarità condizione di lipschitz condizione di normalizzazione condizione di parallelismo tra piani condizione di parallelismo tra rette condizione di parallismo tra rette condizione di perpendicolarità fra due rette condizione di simmetria tra rette parallele condizione necessaria e sufficiente Condizione necessaria e sufficiente affinché una curva sia una retta condizione sufficiente condizioni condizioni al contorno condizioni di Cauchy-Riemann condizioni di cebyscev condizioni di chebyshev condizioni di dirichlet condizioni di Hölder condizioni iniziali condizioni sufficienti ma non necessarie condotto conduttività conduzione del calore conferenze della Macy configurazione a più mondi configurazione di equilibrio confinamento magnetico conflitto nucleare confronto confronto di infinitesimi confronto di infiniti congettura abc congettura di Aizerman Congettura di Andrica congettura di Artin congettura di Bateman Congettura di Birch e Swinnerton-Dyer congettura di Collatz congettura di Glibreath congettura di Goldbach congettura di Kalman congettura di Levy Congettura di Maldacena congettura di Opperman congettura di Poincare congettura di Polignac congettura di riemann Congettura di Taniyama-Shimura congettura di wang Congettura di Yang e Mills congettura forte di Goldbach congiunzione logica congruenza coniche coniglio di zenone connessioni affini connessioni inattese cono cono d’attrito cono-luce conservazione del momento angolare conservazione del momento della quantità di moto conservazione dell’energia meccanica conservazione della quantità di moto conservazione della quantità di moto per un sistema di punti materiali conservazione energia totale contagi contagiati contagiati totali contagio contenitore cilindrico contingency angle continuità continuità dell’inversa continuità uniforme contour plot contourplot contrappesi contrappeso contrazione contro-corrente controimmagine controlli automatici Controllo dei reattori nucleari converge o diverge questa serie numerica? convergenza Convergenza assoluta convergenza di una serie convergenza in modulo convergenza non assoluta Convergenza per x che tende all’infinito convergenza puntiforme convergenza puntuale convergenza totale di una serie di funzioni convergenza uniforme convezione forzata convoluzione coordinata temporale coordinate cartesiane coordinate cilindriche coordinate curvilinee coordinate curvilinee ortogonali coordinate dell’astronavigatore coordinate normali coordinate polari coordinate polari nel piano coordinate polari nello spazio coordinate sferiche Copenhagen interpretation copiare coppie di cooper coppie di Goldbach coppie ordinate coppie virtuali coranavirus corda corda omogenea corea del sud corollario coromavirus coronaviru coronavirus corpi corpo grigio corpo nero corpo rigido Corrections to the diffusion coefficient of Fick’s law Correzioni al coefficiente di diffusione della legge di Fick corridori corrispondenza corrispondenza inversa corrispondenza tra insiemi corrispondenza univoca corsa campestre corso online corto circuito cos’è il Tempo? coscienza coseno coseno iperbolico Cosmic Background Radiation cosmologia costante di eulero mascheroni costante di Feigenbaum costante di hubble costante di integrazione costante di normalizzazione costante di struttura fine costante di tempo costante di tempo – circuito RL costante elastica costante indeterminata costanti di Stiltjes costanti fisiche fondamentali costruttore universale costruzione grafica con sola riga costruzione grafica della retta polare p di un punto polare P cotangente covettori covid covid è clinicamente morto covid-19 covid-scanner covid19 creazione dell’universo Crescenza e decrescenza di una funzione Crescenza e decrescenza di una funzione reale di variab crescita crescita esponenziale crisi idrica cristalli temporali criteri di convergenza criteri di convergenza assoluta Criteri di regolari Criteri di regolarità per confronto Criteri di regolarità per restrizione criteri di Robin e Lagarias criteri di sommabilità criteri sufficienti Criteri sufficienti di sommabilità criterio del cerchio criterio del confronto criterio del rapporto criterio del rapporto inapplicabile criterio del solo punto critico criterio dell’integrale criterio della radice criterio di Cauchy criterio di confronto criterio di convergenza di Kummer criterio di Popov criterio di Raab criterio di Raabe criterio di tensorialità criterio generale di convergenza uniforme criticità Crittografia crittografia a chiave pubblica cronache del dopobomba crowdfunding ctc cubetto di ghiaccio cubi cubica sghemba cubo cultura scientifica cuori curva Curva di classe C^oo curva di Koch curva di rotazione delle galassie curva di ugual durata curva discriminante curva esponenziale curva generalmente regolare curva logistica curva materiale omogenea Curva non analitica con versore normale non definito curva orientata curva piana curva piana in forma implicita curva regolar curva regolare curva sopraelevata curva sopraelevata con attrito curva tracciata su una superficie curvatura Curvatura della cicloide Curvatura e raggio di curvatura di una curva piana curvature Curvature and radius of curvature of a plane curve Curvature and torsion of the cylindrical circular helix curve curve cicloidali curve di fase curve di livello Curve di livello della funzione zeta di Riemann Curve di livello di funzione reale di due variabili reali curve generalmente regolari curve integrali curve integrali di un campo vettoriale curve parametriche curve piane curve regolari curve separatrici Curve Theory Curves in R³ curvilinear abscissa cuscino di Lissajous cuspide Cuspide o punto di regresso cyberpunk daniele lupo darwin David Bohm David Kaiser davydov de broglie De L’Hopital rule deceduti decessi decessi per coronavirus decomposizione decomposizione in frazioni parziali decomposizione in frazioni semplici Decomposizione LU Decomposizione polare Decomposizione spettrale decremento logaritmico definizione Definizione assiomatica di equazione differenziale ordinaria Definizione di derivata di una funzione reale di variab Definizione di derivata di una funzione reale di variab definizione di insieme Definizione di limite deformazioni degenerazione degeometrizzando eternamente delete delta di dirac delta di dirac discreta delta di Kronecker denaro densità densità degli zeri densità di carica densità di corrente di neutroni densità di corrente neutronica densità di probabilità densità in funzione di costante indeterminata densità media densità spettrale densità superficiale density plot derivabilità derivabilità a sinistra e a destra derivabilità di una funzione e continuità della derivata derivata derivata con mathematica derivata covariante derivata destra derivata di funzioni implicite Derivata di una funzione reale di una variabile reale derivata direzionale derivata in forma parametrica Derivata infinita derivata logaritmica derivata mista del terzo ordine Derivata parziale di una funzione vettoriale derivata prima derivata seconda derivata seconda in forma implicita derivata seconda in forma parametrica derivata secondo una direzione derivata sinistra derivata tensoriale Derivata terza derivata totale derivate con mathematica derivate di ordine superiore derivate parziali derivate parziali del secon do ordine derivate parziali del second’ordine derivate parziali del terzo ordine derivate parziali miste derivate vettoriali notevoli derivato di un insieme derivazione assoluta e relativa di una funzione vettoriale derivazione complessa derivazione di funzioni algebriche derivazione di funzioni composte derivazione di funzioni trigonometriche Derivazione di funzioni varie derivazione numerica derivazione parziale derivazione parziali Derivazione sotto il segno di integrale derivazione termine a termine Derive description determinant determinante determinante di Pochhammer determinante di una matrice quadrata determinante funzionale determinante Jacobiano determinante wronskiano determinanti determinanti del secondo ordine determinismo fisico deutone deviazione deviazione dalla sfericità DFT diagonale diagonali diagonalizzazione diagonalizzazione di una matrice diagramma cartesiano Diagramma di Eulero-Venn diagramma di Nyquist diagramma di Venn diagramma orario diagrammi di venn dicke didattica online diego marin Diffeomorfismi diffeomorfismo differential geometry differenza di due insiemi differenza di pressione” differenza di temperatura media logaritmica differenziabilità Differenziabilità secondo Stolz Differenziale Differenziale del second’ordine Differenziale di funzioni implicite differenziale esatto differenziale secondo differenziale totale differenziale totale del secondo ordine differenziale totale del terzo ordine differenziale totale secondo differenziali esatti diffrazione diffusione di virus digitale dilatazione del tempo dimensione dimensione dei font Dimensione del sottospazio delle matrici a traccia nulla Dimensione dello spazio vettoriale dato dal prodotto tensoriale di spazi vettoriali dimessi Dimostrare per assurdo la congettura di Riemann dimostrazione euristica dimostrazione per assurdo dinamica Dinamica dei sistemi materiali Dinamica del punto materiale dinamica non lineare dinamica nonlineare dinamica unidimensionale Dio non gioca a dadi diodo diodo a giunzione diodo a vuoto Dipendenza e indipendenza lineare dipendenza lineare dipendenza stocastica Dirac direttive bidimensionali direttive grafiche direttive grafiche.graphics direttrice disaccoppiamento dei neutrini disaccoppiamento radiazione materia discesa discontinuità discontinuità apparente Discontinuità della derivata discontinuità delle derivate discontinuità di prima specie discontinuità di seconda specie discontinuità eliminabile discontinuità eliminabili Discontinuity points of a function containing a logarithm discontinuity points of the second kind discriminante disegnare il cremoniano della trave Polonceau Disequazioni Disequazioni con valore assoluto Disequazioni esponenziali disequazioni goniometriche disequazioni in due variabili Disequazioni irrazionali Disequazioni logaritmiche disequazioni nel campo complesso Disequazioni razionali disequazioni razionali fratte Disequazioni razionali intere disequazioni razionali intere di secondo grado Disequazioni trigonometriche disgiunzione logica inclusiva dispense dispersione distacco distanza distanze distribuzione distribuzione beta distribuzione binomiale distribuzione binomiale negativa distribuzione dei numeri primi distribuzione di bose-einstein distribuzione di Cauchy distribuzione di fermi-dirac distribuzione di gauss distribuzione di laplace distribuzione di poisson distribuzione esponenziale distribuzione frattale distribuzione Gamma distribuzione gaussiana distribuzione geometrica distribuzione ipergeometrica distribuzione maxwelliana distribuzione multinomiale distribuzione normale bidimensionale distribuzione normale condizionata distribuzione uniforme distribuzioni condizionate distribuzioni di probabilità distribuzioni marginali distribuzioni marginali e condizionate Distribuzioni statistiche e processi ergodici disuguaglianza di Bessel Disuguaglianza di Cauchy-Schwartz disuguaglianza di Miyaoka disuguaglianza di Schwartz disuguaglianza triangolare disuguglianza di Schwartz divergenza divergenza nulla divisione per zero divisori di Dirichlet DMT dogma domini di coerenza dominio dominio normale dominio normale rispetto all’asse y dominio regolare donna al volante donna isterica al volante doppia fenditura doppio piano inclinato dora Wengtirry douglas hofstadter douglas hoftsdater download dramma gnoseologico dramma teatrale droga dsolve dualismo cartesiano dualismo onda-corpuscolo Dürrenmatt e=mc^2 ebook ebooks ecosistema edificio editor editoria editoria digitale editoria digitale low cost editoria scientifica effetto compton effetto doppler effetto fotoelettrico effetto joule effetto meissner effetto tunnel efficacia efflusso einstein Einstein-Poldosky-Rosen Eisenstein electron elemento d’arco elemento neutro elettrodotti Elettrologia elettrone elettroni elettronica elettrostatica elettrotecnica elica cilindrica elica esponenzialmente smorzata elio saba ellisse ellissi coassiali ellissoide di rivoluzione emozioni endomorfismi Endomorfismi autoaggiunti endomorfismi diagonalizzabili endomorfismi emisimmetrici Endomorfismi nilpotenti endomorfismi normali Endomorfismi unitari endomorfismo Endomorfismo autoaggiunto endomorfismo inverso endomorfismo non singolare Endomorifmo autoaggiunto endothermic reaction energia energia cinetica energia dell’oscillatore armonico energia di coesione energia di fermi energia di legame energia dissipata energia interna energia meccanica energia negativa energia potenziale energia potenziale efficace energia potenziale gravitazionale energia termica energia totale ennio de giorgi enrico fermi entalpia entanglement entanglement quantistico entanglment quantistico enterprise enti fisici enti geometrici entropia entropia negativa enumerate envelope Envelope of a family of plane curves epicicloide epicicloidi epidemia equation normal plane equazione equazione algebrica Equazione critica del modello di Fermi Equazione critica per il metodo “due gruppi” di un reattore riflesso equazione d’onda Equazione d’onda di D’Alambert equazione d’onda di D’Alembert equazione d’onda di Helmholtz equazione del bilancio equazione del covid equazione del moto equazione dell’amore equazione dell’età di fermi Equazione della cicloide equazione della corda vibrante equazione della mediana equazione della retta equazione della retta nel piano equazione delle orbite equazione di bernoulli equazione di Boltzmann equazione di compo equazione di conduzione del calore equazione di continuità equazione di d’Alambert equazione di D’Alembert equazione di diffusione equazione di Drake equazione di Emden-Fowler equazione di eulero equazione di eulero-lagrange equazione di grado n equazione di Hamilton-Jacobi equazione di klein-gordon equazione di Korteweg-de Vries equazione di Lane-Emden equazione di langevin equazione di Laplace equazione di Poisson equazione di riccati equazione di schrödinger equazione di Schrödinger dipendente dal tempo equazione di Schrödinger stazionaria equazione di terzo grado equazione di Thomas Fermi equazione di wheeler de witt equazione differenziale equazione differenziale alle derivate parziali equazione differenziale di bernoulli Equazione differenziale di Emden Fowler equazione differenziale di riccati equazione differenziale lineare omogenea Equazione differenziale ordinaria in forma normale equazione differenziale stocastica equazione differenziale stocastica nonlineare equazione fondamentale della trasmissione di calore per convezione equazione integrale equazione KdV equazione omogenea equazione oraria equazioni equazioni algebriche Equazioni alle differenze equazioni della cinetica equazioni di Cauchy-Riemann equazioni di Einstein equazioni di Friedmann equazioni di Navier Equazioni di Pell-Fermat Equazioni di variabile complessa Equazioni differenziali equazioni differenziali a variabili separabili equazioni differenziali a varibili separabili equazioni differenziali alle derivate parziali equazioni differenziali del primo ordine equazioni differenziali ellittiche equazioni differenziali lineari equazioni differenziali lineari a coefficienti costanti equazioni differenziali lineari del primo ordine equazioni differenziali lineari non omogenee equazioni differenziali non lineari equazioni differenziali ordinarie equazioni differenziali stocastiche equazioni finite del moto equazioni goniometriche equazioni matriciali equazioni non linear equazioni non lineari equazioni operatoriali equazioni orarie equazioni parametriche equazioni parametriche della retta equazioni parametriche della trocoide equazioni parametriche di una retta equazioni razionali equazioni termochimiche equi-corrente equidistanza tra rette parallele equilibri di nash equilibrio equilibrio asintoticamente stabile equilibrio di nash equilibrio dinamico equilibrio instabile equilibrio stabile equilibrio stabile secondo lyapunov equilibrio statico equilibrio statico di un sistema meccanico equilibrio su piano inclinato scabro equilibrio termico equiprobabilità Equivalent parametric representation equivalenza massa-energia era adronica era atomica era delle transizioni di fase era leptonica erasmo falanga erasmo recami erg erie numeriche errore di calcolo errore lineare medio errore quadratico medio errori di compilazione esame esame di Analisi Matematica 1 esame di Fisica 1 esame di maturità esame scritto Esame scritto di Analisi 1 esami esami di maturità escher esempio esercizi esercizi analisi matematica esercizi d’esame Esercizi di autovalutazione Esercizi di Matematica esercizi equazioni differenziali del primo ordine lineari esercizi fisica 1 esercizi meccanica quantistica esercizi svolti esercizi svolti di Fisica Tecnica esercizi svolti integrali esercizi tensori controvarianti esercizi vettori eserciziario esercizio esercizio d’esame di Meccanica analitica esercizio di fisica esercizio di Meccanica analitica fasano marmi esercizio sui vettori controvarianti esercizio svolto Esercizio svolto di Geometria differenziale esercizio svolto su limite di funzione esericizi svolti esistenza e continuità delle derivate esonero analisi matematica 1 espansione espansione isotermica di un gas perfetto esperienza della doppia fenditura esperimenti computazionali esperimento computazionale esperimento del secchio di Newton esponenziale esponenziale complesso esponenziale integrale estate estensione complessa Estensione di Goldbach Estrazione di una potenza di x da una radice di indice estremi assoluti Estremi assoluti di una f(x) estremi di un insieme estremi di una funzione di due variabili estremi di una funzione reale di una variabile reale estremi relativi Estremi relativi di una f(x) estremi relativi ed assoluti estremi vincolati estremo inferiore estremo superiore età dell’universo età di fermi etilene gassoso ettore majorana ettore majorna Euclide eventi evento everett evoluta Evoluta dell’iperbole Evoluta della parabola Evolution evoluzione termica dell’universo prima del disaccoppiamento evoluzionismo evolvente Exercise of Differential Geometry exercises in differential geometry Exercises in nuclear reactor physics Existence and Uniqueness exothermic reaction fabrizio coppola facebook fallimento del criterio del solo punto critico falsificazionismo falsificazionismo di Karl Popper famiglia famiglia di curve piane famiglia di insiemi fantappiè fantascienza fantasma di hilbert farfalla di Hofstadter fasano marmi fascio di rette fase 2 Fattore di utilizzazione termica fattore f fattore integrante fattore p Fattore razionalizzante fattori fattoriale fattoriale della parte intera di x fattoriale di n fattoriale inverso fattorizzazione fattorizzazione di Repunit febbre di gaia felini fenditura fenomeni paranormali fenomeno di gibbs fenomeno di Lehmer fenomeno di runge FFT fibonacci Fibra di un’applicazione fibrato tangente figura piana figure figure di lissajous film film sincronicity filo filo inestensibile filosofia filosofia della scienza filosofia e religione filtri di Chebyschev filtro passa basso finanziamenti Finding a Level Curve fine del mondo fine dell’energia finestra del visibile fiocco di neve fiori firma virale firmamento first fisica fisica 1 fisica del nucleo fisica del nulla fisica del reattore nucleare fisica dell’immortalità Fisica generale 1 Fisica generale 2 Fisica lisergica. La mente profonda e la struttura dell’Universo fisica quantistica fisica tecnica fisica tenica fisica teorica fisico fisico teorico fissione fissione nucleare fit fitting fixed point fixed points flaccavento flat curve flesso flesso a tangente verticale floor florenskij fluido fluido gassoso flussi hamiltoniani flusso flusso asintotico flusso di calore flusso di neutroni Flusso di un campo vettoriale flusso di un vettore flusso hamiltoniano flusso neutronico focalizzazione magnetica focardi focolai focolai di Hausdorff focus forma algebrica forma bilineare Forma canonica di Jordan forma cartesiana forma complessa Forma covariante dell’equazione di Klein-Gordon forma d’onda forma differenziale lineare forma differenziale quadratica forma implicita forma indeterminata Forma indeterminata 0 forma indeterminata 0/0 forma indeterminata 1 elevato a infinito Forma indeterminata 1^oo forma indeterminata infinito elevato a zero forma indeterminata infinito meno infinito forma indeterminata infinito su infinito forma indeterminata infinito-infinito Forma indeterminata oo forma indeterminata oo-oo Forma indeterminata oo/oo Forma indeterminata risolvibile con limiti notevoli Forma indeterminata risolvibile con un cambio di variabile forma indeterminata uno elevato a infinito forma indeterminata zero elevato a zero forma indeterminata zero per infinito forma indeterminata zero su zero forma indetermintata forma integrale forma integrale delle equazioni del moto forma lineare forma operatoriale forma trigonometrica formal logic formal system FORMAT formati numerici formato dei numeri formato numeri formattazione formattazione dei testi forme 1-lineari Forme bilineari Forme differenziali forme differenziali lineari forme differenziali quadratiche Forme indeterminate forme lineari forme quadratiche forme reali forme sesquilineari formica di coriolis formula di Amitrano formula di binet formula di Cauchy formula di decomposizione di un infinitesimo formula di decomposizione di un infinito formula di erone Formula di Eulero formula di Grassmann formula di moivre formula di riemann von mangoldt formula di stirling formula di Taylor formula fondamentale del calcolo integrale formulario formulazione di Oesterlè formule di bisezione formule di duplicazione formule di green formule di green nel piano formule di poisson formule di prostaferesi formule di riduzione formule di riduzione integrale doppio formule di riduzione integrali doppi formule di Werner formule fondamentali di integrazione formule parametriche formule trigonometriche Fortran forza forza centrale forza centrifuga forza centripeta forza costante forza d’attrito forza di inerzia forza elastica forza elastica di richiamo forza elastiche forza esercitata da una fune forza gravitazionale forza periodica forza peso forza trainante forza viva forze forze attive forze centrifughe forze conservative forze d’inerzia forze di attrito forze dipendenti dalla velocità forze elastiche forze esterne forze interne forze non conservative forze posizionali foto Fotogrammi spaziotemporali fotone fourier foze interne francisco varela Frank Tipler franz kafka frattali frattalità freccia freccia del tempo freccia del tempo termodinamica frenet formulas Frenet’s theorem freni ad aria compresso freno frequenza frequenza variabile frequenze normali Friedrich Dürrenmatt frigorie fritjof capra frontespizio frontiera di un insieme frontiera dominio fucile fuel burn up fuel material fune fune ideale fune inestensibile fune inestensibile e di massa trascurabile fune omogenea funzionale funzionale lineare funzionali funzionali lineari funzione funzione analitica Funzione che tende a un limite l per valori maggiori di funzione che tende all’infinito Funzione che tende all’infinito per x tendente all’infinito funzione continua Funzione convergente all’infinito funzione costante funzione crescente funzione d’onda Funzione d’onda di una particella localizzata in un punto funzione d’onda di una particella relativistica di spin 0 funzione decrescente funzione degli errori funzione delta di dirac funzione di Airy funzione di autocorrelazione funzione di Chebyscev funzione di distribuzione funzione di distribuzione a gradino funzione di due variabili funzione di hamilton funzione di hardy funzione di Heaviside funzione di lambert funzione di più variabili funzione di riemann funzione di riemann siegel funzione di Riemann-Siegel-Hardy funzione di todd funzione di variabile complessa funzione dispari funzione dissipativa funzione divergente positivamente funzione esponenziale funzione esponenziale integrale funzione gamma funzione generalmente continua funzione identica funzione identicamente nulla funzione infinitesima funzione integrabile funzione integrale funzione intera funzione inversa funzione irrazionale funzione localmente invertibile funzione logaritmo funzione monotona funzione mu funzione non derivabile funzione non periodica funzione non regolare funzione opposta funzione pari funzione parte intera funzione parte intera di x funzione periodica funzione polinomio funzione potenza funzione potenza di esponente reale funzione potenza di esponente reale negativo funzione primitiva funzione razionale funzione reale di due variabili reali funzione reale di una variabile reale funzione reciproca funzione round funzione scalare funzione signum funzione sin(1/x) funzione sinc funzione sinc(x) funzione sinx” funzione sommabile funzione trigonometrica funzione trigonometrica inversa funzione unit step funzione valore assoluto funzione vettoriale funzione vettoriale di una variabile reale Funzione vettoriale localmente limitata funzione vuota funzione xi di riemann funzione zeta funzione zeta alternata funzione Zeta di Riemann funzione zeta di riemannn funzione zeta nel campo reale funzioni Funzioni a valori vettoriali funzioni alfa-hölderiane funzioni analitiche funzioni armoniche funzioni associate di legendre funzioni booleane funzioni circolari funzioni circolari intere funzioni circolari inverse Funzioni complesse funzioni composte funzioni continua Funzioni continue Funzioni continue (in più variabili) funzioni convergenti all’infinito funzioni convesse funzioni crescenti funzioni crescenti e decrescenti in un punto funzioni d’onda funzioni debolemente analitiche funzioni decrescenti funzioni definite dall’utente funzioni derivabili funzioni di bessel funzioni di complessità funzioni di dominio funzioni di due variabili funzioni di matrici funzioni di modulo quadro sommabile funzioni di n variabili Funzioni di n variabili reali funzioni di più variabili funzioni di segno variabile funzioni di tre variabili Funzioni di una variabile complessa funzioni di variabile complessa funzioni di variabili aleatorie funzioni differenziabili funzioni dispari funzioni elementari funzioni esponenziali funzioni esponenziali e logaritmiche funzioni forma indeterminata 1 elevato a infinito funzioni forma indeterminata zero su zero funzioni generalmente continue funzioni goniometriche inverse funzioni implicite funzioni integrabili Funzioni integrali funzioni iperboliche funzioni iperboliche inverse funzioni irrazionali Funzioni L p-adiche funzioni lipchitziane funzioni Lipschitziane funzioni logaritmiche funzioni monotone funzioni monotone in un intervallo funzioni non elementarmente esprimibili funzioni non integrabili funzioni non lineari senza memoria funzioni non regolari funzioni olomorfe funzioni omogenee funzioni pari Funzioni periodiche funzioni primitive funzioni razionali funzioni razionali fratte funzioni reali Funzioni reali di n variabili reali Funzioni reali di una variabile reale funzioni regolari Funzioni ricorsivamente convergenti Funzioni ricorsivamente divergenti funzioni ricorsive Funzioni sommabili funzioni trigonometriche funzioni trigonometriche inverse funzioni vettoriali Funzioni vettoriali di una variabile vettoriale funzioni vettoriali lineari fusione fredda fuso orario futuro assoluto fuzzy logic G5 gabbiani gabbiano gabriella greison gaeta Gaetano Fichera galassia galassie galilei galleggiamento galvanometro game of life gamma symbols gantmacher gas gas di bose gas di elettroni relativistici degenere gas di fermi gas di fermi degenere gas perfetto gattino gatto gatto di schödinger gatto di schrödinger gaussiana gaussiane Generare una lista di rettangoli random con Mathematica generatore delle traslazioni spaziali generatori di f.e.m. generatrici genere geni genio matematico Geometria geometria 1 geometria 2 geometria affine geometria algebrica Geometria analitica Geometria computazionale Geometria convessa Geometria differenziale Geometria frattale Geometria II Geometria III Geometria proiettiva geometria riemanniana Geometria simplettica geometric interpretation of the Frenet formulas ghizzetti giganti gilda senatore giochi matriciali gioco a somma zero gioco del caos gioco del lotto gioco di dadi gioco mu giocoliere giorgio parisi giove gittata gittata massima giuliano preparata giunto Given a smoot non analytic curve GLPK gmailtex GNU Octave GNUPLOT goal god like gödel gplot gradiente gradino unitario grafica grafica tridimensionali grafici grafici di funzioni grafico grafico di una funzione Grafico di una relazione grafico funzione grafico funzione di due variabili grafite grafo gram points grammofono grande contagio grandezze periodiche GraphicsArray gravità gravitazione Gravitazione universale Grigorij Jakovlevic Perel’man grinding plane grof Grothendieck Grigorij Jakovlevic Perel’man gru gruppi armonici gruppi di coerenza gruppi di Lie gruppi topologici gruppo gruppo delle applicazioni bi-iettive gruppo delle sostituzioni gruppo di neutroni ritardati gruppo facebook gruppo ortogonale Gruppo U(n) delle matrici unitarie. Sottogruppo SU(2) di U(2) gruppoidi Guadagno da riflettore (reflector saving) guarigione guariti guerra atomica guida guida a mathematica Guida a Mathematica in italiano Gunnar Gohl gusci hackers hackers gli eroi della rivoluzione informatica halliday resnick halloween hamiltoniana hamiltoniano Hans Riesel hardy hartle-hawking hausdorff heisenberg heisenberg-indeterminismo-gödel-indecidibilità-idealismo hessiano hilbert hofstadter hoftsdater hospital How do you find the envelope of a family of curves? Hugh Everett Hugh Everett III humberto maturana I am a strange loop i fisici i grandi della scienza i primi tre minuti identità di parseval identità fondamentali idrodinamica Il caso Majorana il coniglio di zenone Il favoloso mondo della Fisica quantistica Il fenomeno di Lhemer e gli zeri apparenti della zeta di riemann il figlio del tempo il genio dei numeri Il genio dei numeri. Storia di John Nash Il grande contagio il paziente e l’analista Il segreto dell’universo Il tempo vuole uno scheletro il teorema di cambridge imiti imiti di funzioni esponenziali immagine Immagine di un’applicazione Immagine di un’applicazione vettoriale immagine inversa immediata immortalità quantistica impatto con la Terra imprecazione impulso impulso di fermi Impulso di una forza incognite incompletezza incremento Incremento di una funzione Incremento di una funzione reale di una variabile reale indecidibilità indeterminazione indeterminismo indicatore logaritmico indice di positività indipendenza stocastica induttanza inegrali tripli inequazioni inestensibile infinite infinitesimi infinitesimi confrontabili infinitesimi dello stesso ordine infinitesimi di ordine infinitamente grandi infinitesimi di ordine infinitamente piccolo infinitesimi di riferimento Infinitesimi ed Infinitesimi ed infiniti infinitesimi ed infiniti di ordine indeterminato infinitesimi non confrontabili infinitesimi non dotati di ordine infinitesimo infinitesimo di riferimento infiniti infiniti di ordine infinitamente grandi infiniti di ordine infinitamente piccolo infiniti non dotati di ordine infiniti punti di discontinuità infinito di riferimento influenza informatica information wants to be free informazione ingegnere chimico Colburn ingegneria industriale iniettività globale iniettività locale inkscape insetto insieme insieme aperto insieme chiuso insieme complementare insieme delle parti insieme di cantor Insieme di definizione insieme di livello insieme di Mandelbrot insieme perfetto insieme ricorsivo insieme vuoto insiemi insiemi compatti insiemi illimitati insiemi in estensione insiemistica instabilità asintotica integ integer part integrabilità integrabilità di una forma differenziale lineare integrale Integrale con esponenziale Integrale con esponenziali integrale curvilineo integrale curvilineo complesso integrale definito integrale della funzione di gauss integrale di circuitazione integrale di Eulero integrale di fermi integrale di Lebesgue integrale di linea integrale di mengoli-cauchy integrale di riemann integrale di superfice integrale di superficie integrale di un vettore Integrale di una funzione reale di una variabile reale Integrale di una funzione reale di variabile reale integrale doppio integrale fasano-marmi integrale gaussiano integrale generale integrale generale in forma implicita integrale generalizzato integrale guassiano generalizzato integrale indefinito integrale primo del moto Integrale primo dell’energia Integrale primo delle forze vive integrale principale di Cauchy integrale singolare integrale trigonometrico Integrali integrali con Mathematica integrali con valore assoluto Integrali contenenti un trinomio di 2^ grado integrali curivilinei Integrali curvilinei Integrali definiti integrali di circuitazione integrali di fourier Integrali di Fresnel integrali di funzioni esponenziali Integrali di funzioni iperboliche Integrali di funzioni irrazionali integrali di funzioni logaritmiche Integrali di funzioni razionali Integrali di funzioni razionali fratte Integrali di funzioni trascendenti integrali di funzioni trigonometriche integrali di superfici Integrali di superficie integrali doppi integrali ellittici Integrali ellittici di prima specie integrali ellittici di seconda specie integrali ellittici di terza specie integrali fondamentali Integrali generalizzati integrali impropri Integrali indefiniti integrali multipli integrali notevoli integrali pseudoellittici integrali singolari Integrali trigonometrici Integrali tripli integrazione Integrazione dell’equazione di Fermi” integrazione di Stieltjes Integrazione di varie funzioni trascendenti Integrazione diretta integrazione equazione di diffusione integrazione forme differenziali integrazione forme differenziali lineari integrazione immediata integrazione numerica integrazione per decomposizione Integrazione per parti integrazione per quadrature integrazione per sostituzione Integrazione per trasformazione di coordinate integrazione termine a termine intelligenza intelligenza artificiale intensità di corrente interazione amorosa interconnessione di sistemi interi naturali interi relativi internet of things interno di un insieme interpolatingfunction interpolazione interpolazione polinomiale interpretazione a più mondi interpretazione di bohm interpretazione di Copenaghen interpretazione di david bohm interpretazione di David Bohm della meccanica quantistica interpretazione di schwinger Interpretazione fisica degli zeri della funzione Zeta di Riemann interpretazione geometrica Interpretazione geometrica della regola di De L’Hospital Interpretazione ondulatoria della meccanica interruttori Intersection of a cylinder with a plane intersezione intersezione di due rette Intersezione di un cilindro con piano Intersezione di un piano con un cilindro intersezioni con gli assi intervallo base intorni intorni disgiunti intorno intorno sferico introduzione Introduzione all’analisi matematica Introduzione alla Fisica del reattore nucleare Introspezione cosmica invariante integrale di poincare-cartan invecchiamento inversa locale invertibilità invertibilità dell’ordine di derivazione parziale invertibilità locale funzioni trigonometriche inviluppo inviluppo di modulazione inviluppo di una famiglia di curve piane Inviluppo di una famiglia di rette iperbole equilatera iperboli equilatere iperboloide di rivoluzione iperboloide rotondo ipersuperfici di livello ipocicloide ipocicloidi ipotesi di De Broglie ipotesi di Riemann ipotesi di riemnn ipotesi intelligenza artificiale forte irraggiamento irraggiamento termico isaac asimov isaac newton isaacn newton isola di koch isometria isomorfismi isomorfismo istanti di arresto istanti di arresto con inversione del moto Istituzioni di matematica itemize iterazione Jack lo strangolatore jacobiano jacques monod Java applet Javascript jessica John Hagelin John Nash join Jooble joule julia julian barbour julian borbour Jung kafka Kalman-Yakubovic-Popov Lemma kant karl popper kauffman kernel ket ket di stato kinetic energy knuth koan zen korobov Kurt Gödel l prodotto scalare quale tensore covariante di rango 2 L’enigma dei numeri primi L’evoluta di un asteroide è un asteroide L’indistinguibilità delle particelle in Meccanica quantistica L’ultimo teorema di Fermat l’uomo che vide l’infinito la cattedra vacante la dinamica del clima La distribuzione dei numeri primi e la Meccanica quantistica la fine del tempo La forma indeterminata uno elevato a infinito la formula di Euler-MacLaurin La formula di Nielsen-Ramanujan la mela di Turing la mente nuova dell’imperatore la rete della vita La Scienza sa di non sapere. Per questo funziona La scoperta del neutrone la strada che porta alla realtà la-formula-di-inversione-di-mobius-e-la-formula-di-riemann-von-mangoldt lagrange lagrangiana lambert function lampada lampadina lampert lancio del peso lancio di dadi lancio di monete landau langevin laplace laplaciano last lastra lastra di alluminio LaTeX lati lato laurea lavoro lavoro delle forze di attrito lavoro di una forza lavoro eseguito da una forza lavoro meccanico Lawrence e Oppenheimer; layout Le 17 equazioni che hanno cambiato il mondo Le funzioni di Lyapunov Le Scienze legge del terzo escluso legge di dispersione legge di distribuzione dei numeri primi legge di fick legge di fourier legge di Gauss legge di hooke legge di Hubble legge di joule legge di murphy legge di ohm legge di trasformazione leggi di composizione leggi di keplero leggi di newton lem lemma del piccolo e grande cerchio lemma di Coriolis lemma di Jordan lemniscata di Bernoulli Length of a curve Length of an arc of a curve Leonardo Sciascia Lepidoptera leslie lamport letalità letargia Levi-Civita lezioni lezioni di meccanica analitica lezioni private libero arbitrio Libri libro liceo scientifico limit of the topologist limitata limite limite all’infinito limite del prodotto di due funzioni Limite del rapporto incrementale limite del topologo limite della somma di una serie di funzioni limite destro limite di funzione Limite di funzione trigonometrica limite di successione Limite di una funzione per x che tende all’infinito limite di una funzione reale di una variabile reale Limite di una funzione vettoriale limite di una funzione vettoriale di una variabile vettoriale limite fondamentale limite funzione più variabili limite infinito limite non esiste limite per x che tende a infinito limite per x che tende a zero limite rapporto incrementale limite sinistro limite sinitro Limite successione di funzioni limiti limiti con mathematica Limiti delle funzioni iperboliche Limiti delle funzioni iperboliche e delle funzioni iperboliche inverse Limiti delle funzioni iperboliche inverse Limiti delle funzioni iperboliche inverso limiti di funzioni Limiti di funzioni di più variabili limiti di funzioni esponenziali Limiti di funzioni esponenziali e logaritmiche Limiti di funzioni esponenziali ed iperboliche limiti di funzioni irrazionali Limiti di funzioni irrazionali. La forma indeterminata oo-oo e il fattore razionalizzante limiti di funzioni logaritmiche Limiti di funzioni reali di più variabili Limiti di funzioni reali di una variabile reale limiti di funzioni trigonometriche limiti di funzioni trigonometriche inverse limiti di successioni limiti fondamentali limiti funzioni irrazionali limiti funzioni trigonometriche inverse limiti notevoli limiti parametrici linea critica linearsolve linearsolvefunction linee coordinate linee di forza linee vettoriali linguaggio liniti lipschitz liquido lisp liste localismo lockdown locomotore logaritmi logaritmo logaritmo integrale Logica Matematica logistica lombardia loop Do loop quantum gravity loop transformation lord axel lossodromia lotto LSD luce solare Luci di Hessdalen Ludwig von Bertalanff Luftkissenfahrzeug luhmann luigi fantappiè luna cade sulla terra luna park lunghezza lunghezza arco lunghezza arco di curva lunghezza d’onda di Jeans lunghezza di planck lunghezza di un arco di curva regolare Lur’e problem Lyapunov ma con somma continua ma non analitica macchina macchina del tempo macchina della Realtà macchina di Atwood macchine a stati finiti macchine frigorifiche macchine molecolari macchine operatrici macchine ricorsive macchine ricorsive topologiche macchine termiche mach macsyma maggiorante maggiorazione del resto maglie mail majorana malattia Mandelbrot mandò mani che disegnano manoscritti inediti manuale Many Wolrds Interpretation many worlds interpretation map Maple mappa mappa logistica mappe cognitive fuzzy marcello colozzo Marcus Du Sautoy Marcus-Yamabe Conjecture marika Maryam Mirzakhani mascherina Mass Defect and Binding Energy massa massa critica massa di ossigeno massa di planck massa inerziale massa solare massimo massimo assoluto massimo citro massimo relativo massimo relativo improprio massimo relativo proprio massimo teodorani matehmatica matematica Matematica A matematica applicata matematica B matematica combinatoria Matematica discreta Matematica finanziaria matematica open source matematicamente matematico matematico e folle materia oscura materia vivente materiale fissile materiali superconduttori Mathemati mathematic Mathematica Mathematical Foundations of Quantum Mechanics mathgirl Mathics matla Matlab Matri matrice matrice aggiunta matrice anti-hermitiana matrice antisimmetrica matrice di rigidezza matrice di rotazione matrice diagonale a blocchi matrice hermitiana matrice idempotente matrice inversa matrice involutoria matrice jacobiana matrice metrica matrice nilpotente matrice normale matrice ortogonale matrice quadrata matrice rappresentativa matrice scalare matrice simmetrica matrice trasposta matrice triangolare alta matrice triangolare bassa matrici matrici a traccia nulla matrici che commutano matrici commutanti matrici di pauli Matrici di rotazione e curve cicloidali Matrici e determinanti matrici hamiltoniane matrici ortogonali matrici quadrate matrici simili matrici simmetriche matrici unitarie matrix laboratory Matura Camp maturana maturana-varela mauro biglino max born max planck” maxima maxwell-boltzmann Meccanica meccanica analitica meccanica classica Meccanica dei corpi rigidi meccanica dei fluidi meccanica dei sistemi di punti materiali meccanica delle collisioni elastiche meccanica delle matrici meccanica ondulatoria meccanica quantistica meccanica razionale meccanica statistica medaglia fields media artimetica media integrale mediana medicina sistemica mela melatonina memoria mente e materia nella scienza del terzo millennio mesh rettangolare MeshMaker Messiah metafisica metarealismo metastasi Metodi degli elementi finiti metodi di integrazione metodi matematici metodi numerici metodo degli elementi finiti Metodo dei coefficienti indeterminati metodo dei gusci cilindrici metodo dei minimi metodo dei minimi quadrati metodo dei moltiplicatori di lagrange metodo del cerchio metodo del kernel metodo del simplesso metodo di cauchy Metodo di eliminazione di Gauss metodo di Eulero metodo di fourier metodo di gau metodo di gauss Metodo di Gauss-Seidel metodo di hartree-fock Metodo di Jacobi metodo di König-Lemaray metodo di lagrange metodo di Ostrogradskij Metodo di Richardson metodo di Seidel metodo di variazione delle costanti arbitrarie metodo galileiano metodo induttivo metodo scientifico metrica metrica di Finsler metrica di gödel metrica di Minkowsky metrica di Riemann metrica di robertson walker mezzo viscoso microdinamica sociale microonde microsoft word miglioramento miktex mind training minimo minimo relativo minimo relativo improprio minimo relativo proprio minorante minore estratto minori estratti miscela miscele di aria e vapor d’acqua miscele di gas e vapore missile missili v2 misura misura degli insiemi piani misura di una osservabile misura meccanica quantistica misura secondo Peano-Jordan misurabilità dell’insieme di cantor MIT MIT OpencourseWare mitragliatrice di einstein Modelli cosmologici di Friedmann modelli di friedmann modelli epidemiologici modelli matematica modelli matematici modelli matematici pandemia modelli predittivi modello di Bohr dell’atomo di idrogeno modello di thomas fermmi modello preda predatore modello preda-predatore di Lotka-Volterra modello thomas fermi modulazione d’ampiezza modulazione di ampiezza modulo modulo di un vettore molecola biatomica molecole molla molla ideale molluschi moltiplicatore di Popov moltiplicazione righe per colonne momento angolare momento assiale momento assiale della quantità di moto momento assiale di un vettore applicato momento d’inerzia momento della quantità di moto momento di inerzia momento di inerzia di un sistema di punti materiali momento di una forza rispetto a un punto momento di una forza rispetto ad un asse momento polare di un vettore applicato momento risultante momento statico monoidi monomolecular element monotonia montacarichi monte orlando morte cognitiva morte del tempo morti mosca moti di librazione moti periodici unidimensionali moti relativi moti superluminali moti unidimensionali moti uniformemente accelerati moto moto armonico moto asintoticamente uniforme moto bidimensionale moto browniano moto circolare moto circolare uniforme moto dei proiettili moto del centro di massa moto di fluidi moto di proiettili moto di rivoluzione della terra moto di un proiettile moto in un campo centrale moto incipiente moto inerziale einsteiniano moto periodico moto piano moto relativo moto rettilineo ed uniforme moto rettilineo uniforme moto rettilineo uniformemente accelerato moto su traiettoria rettilinea moto superluminale moto unidimensionale moto unidimensionale in un campo conservativo moto uniformemente accelerato moto uniformemente ritardato motore a scoppio motore diesel motori di ricerca movimento romantico mozzo di legno mu puzzle multiverso MuPAD muro murphy’s law musica n fattoriale n-ple ordinate nabla nana bianca nanoaparticelle narcissus nastro di möbiu nastro di möbius nastro di moebius natura Natural parametrization of curves Natural representation of a curve nature of spirit nave fantasma navicella spaziale navigatore inerziale navigatori navigazione navigazione inerziale ndsolve nebulosità quantistica negazionisti covid nemeri primi cubani neonegazionismo neoplatonismo neopositivismo neopositivismo logico nessi acausali nestlist Netsukuku neuromante neurosoma neutrini neutrini superluminali Neutrino elettronico con potenziale chimico non nullo neutron neutrone neutroni isoenergetici neutroni lenti neutroni ritardati neutroni pronti neutroni termalizzati neutroni termici neutroni termini neutroni veloci News&Update newton nfinitesimi niels bohr nnumeri di fibonacci nodal noise non ammette limite Non applicabilità del procedimento di ortogonalizzazione di Gram-Schmidt Non applicabilità della regola di De L’Hospital non commutatività non commutativo non integrabilità non-trivial zeros norbert wiener norma Norma di un vettore norma euclidea normal plane normale normalizzaione norton starr norvegia notazione apicale di Lagrange notazione di dirac notazione di iverson Notazione di Leibnitz notazione matriciale nozioni di base ntegrali doppi Nuclear binding energy Nuclear Reactor Physics nucleo nucleo di Dirichlet nucleo risolvente nucleoni nullità nullspace numeri Numeri casuali Numeri complessi numeri di bernoulli numeri di euclide Numeri di Fermat numeri di Fibonacci numeri di Hailston numeri di Keith Numeri di Lucas Numeri di Mersenne numeri direttori numeri formosi numeri interi naturali numeri irrazionali numeri perfetti numeri periodici numeri primi Numeri primi circolari numeri primi di chen Numeri primi di Cullen numeri primi di euclide Numeri primi di Fermat Numeri primi di Mersenne Numeri primi euclidei numeri primi gemelli Numeri primi omirp Numeri primi ostinati numeri razionali numeri reali numeri RSA numeri semiprimi Numeri triangolari numero di avogadro numero di nepero numero di Skewes numero e odifreddi oggettivazione oggetto appeso Olimpiadi della Matematica olismo olomorfia olone omeomorfismi omeomorfismo omomorfismi omomorfismo onda di materia onda di probabilità onda piana onda pilota onda quadra onda solitaria onda stazionaria Onda stazionaria generalizzata onda termica onde anticipate onde di de broglie onde elettromagnetiche Onde in mezzi elastici onde meccaniche onde piane onde sonore onde stazionarie onde vuote ongettura di riemann ontologie open source operatore aggiunto operatore di derivazione operatore di distruzione operatore di evoluzione temporale operatore di proiezione operatore di scambio operatore differenziale operatori hermitiani operatori lineari operazione di misura Operazione Paukenschlag> operazioni elementari operazioni razionali sulle funzioni operazioni sugli insiemi operazioni sulle liste orbita orbita aperto orbita chiusa orbita circolare orbita geostazionaria orbite circolari orbite circolari perturbate ordinata ordine ordine di un infinitesimo orientabilità origins of order orizzonte cosmologico orizzonte di particella orthogonal group O(n) orthogonal matrix ortodromia ortogonalità Ortogonalizzazione di Schmidt Ortonormalizzazione di Gram-Schmidt oscillatore anarmonico oscillatore armonico Oscillatore armonico a frequenza variabile oscillatore armonico bidimensionale Oscillatore armonico di frequenza aleatoria oscillatore armonico ideale oscillatore armonico in Meccanica classica oscillatore armonico smorzato oscillatore armonico tridimensionale oscillatore armonico tridimensionale isotropo oscillatore armonico unidimensionale oscillatore di duffin oscillatore n-esimo oscillatori accoppiati oscillazione oscillazioni forzate oscillazioni libere Osculating circle osculating plane osservabile osservabile impulso osservabile quantistica osservabili osservabili quantistiche osservatore ottimizzazione motori di ricerca Oxford Murders – Teorema di un delitto oxigen P =NP pacchetti pacchetto d’onde Pacchetto d’onde coerente pacchetto d’onde di minima indeterminazione pacchetto d’onde gaussiano Package palestra rettangolare palla palla di cannone palla di gomma palla di piombo pallina pallina di acciaio palline pallon pallone pandemia pandemic parabola parabola cubica parabola di sicurezza parabola semicubica parabole di neil paraboloide paraboloide ellittico paraboloide iperbolico paraboloide rotondo paracadute paradigma paradossi paradossi percettivi paradosso dei gemelli paradosso dei relativi quadrati paradosso del gatto di boltzmann paradosso del gatto di Schrödinger paradosso del nonno paradosso dell’amico di wigner paradosso della misura paradosso di epimenide paradosso di incoerenza paradosso di russel paradosso di tolman paradosso di zenone paradosso EPR paradosso gatto di schrödinger parallelogramma parametri ParametricPlot parametrizzazione dell’orbita parametrizzazione di SU(2) parametrizzazione naturale parametro parametro d’urto Pardosso EPR parete PARI/GP parità parola di scienziato parte immaginaria parte principale parte principale di cauchy parte principale di un infinitesimo parte principale di un infinito parte reale partial derivative particella particella di Higgs particella in una scatola particella libera particella su un segmento Particella vincolata a muoversi sulla superficie interna di un cono particelle Particelle elementari come microuniversi particelle identiche particelle indistinguibili partizioni Partizioni di numeri passaggio a coordinate polari passato assoluto passo passo dell’elica Patch test path pathological curves paul davies Paul Ehrenfest Pauli pauli e jung un confronto tra materia e psiche Pauli e Jung. Un confronto su materia e psiche pavimento liscio payoff pazzia PDE pendoli accoppiati pendolo pendolo balistico pendolo conico pendolo doppio pendolo in un ascensore pendolo matematico pendolo obliquo pendolo parabolico pendolo semplice pendolo smorzato penrose pensieri pensieri degli anni difficili pensilina penzias Perché la Luna non cade sulla Terra? perché non sono cristiano pericentro perimetro periodicità periodicità del moto” periodo periodo del reattore periodo fondamentale permutazione perpendicolari peso peso apparente Peter Samson pettine di dirac Philippe Pradat pi greco pianeta pianeta decimo piano cartesiano piano delle fasi piano di fano piano inclinato piano inclinato liscio piano inclinato scabro piano isotropo piano orizzontale piano orizzontale scabro piano osculatore piano tangente piano uniformemente carico piastrellatura piastrellatura del piano picche neri piccioni picco picco massimo piccole oscillazioni piccolo guadagno piecewise Piecewise functions pinacoteca gaeta pinochet pioggia pirenei pitagora plasma platonia plot plotino il giovane plotting plutone” pneumatici poeta atemporale poeti polarplot poligoni polinomi polinomi di Bernstein polinomi di Chebyshev polinomi di hermite Polinomi di Legendre polinomi di Taylor polinomi di Tchebichef polinomi trigonometrici polinomiale polinomio Polinomio caratteristico polinomio complesso polinomio di taylor polinomio di Vamanamurthy polinomio minimo polistirolo politropica polizia ponte di einstein-rosen popolazione popolazione virtuale porta AND porta OR portanza portata porte logiche Positive Real Lemma posizione posizione di equilibrio instabile posizione di equilibrio stabile Posizione limite della retta secante posizioni di equilibrio posizioni di equilibrio stabile potenza potenza di rumore potenza dissipata potenza dissipata da una lampadina potenza ennesima potenza istantanea potenza media Potenza sviluppata da un reattore nucleare potenza utile potenziale potenziale centrifugo potenziale chimico potenziale coulombiano potenziale di Heaviside potenziale di Lennard-Jones potenziale gravitazionale potenziale scalare potenziale scalare uniforme potenziale vettore potere assorbitivo potere calorifico potere di rallentamento potere emissivo pozzo Pr0gett0 Al3ph preambolo precipizio precisione di macchina precisione macchina predicatori quantici Predictive Mathematical Models premio nobel prepend pressione pressione costante pressione di equilibrio prgrammazione non lineare prigogine prima forma dell’equazione delle orbite prima legge di keplero prima proiezione primalità primalità di 1 primi di fibonacci primitiva primitiva locale primitive grafiche primo principio della dinamica primo principio di Kirchhoff primo teorema di cauchy principi di Kirchhoff principi variazionali principio antropico principio cosmologico principio dei moti relativi principio del rasio di occam principio del rasoio di Occam principio delle probabilità totali principio di autoconsistenza di novikov principio di azione e reazione principio di causalità Principio di conservazione del momento angolare principio di conservazione del momento della quantità di moto principio di conservazione dell’energia Principio di conservazione della quantità di moto principio di dualità principio di equivalenza principio di funzionamento principio di general-covarianza principio di identità dei polinomi principio di indeterminazione principio di indeterminazione di Heisenberg principio di indistinguibilità Principio di induzione principio di inerzia principio di località di Einstein principio di mach principio di relatività galileiana principio di sincronicità principio di sostituzione degli infinitesimi principio di sostituzione degli infiniti principio di sovrapposizione lineare degli effetti principio evolutivo principio olografico probabilità probabilità di fuga alla risonanza Probabilità discreta Problema «farfalla» problema ai limiti problema degli asini problema degli n corpi problema dei due corpi problema dei quattro colori problema del matrimonio problema delle condizioni iniziali problema dello zaino Problema di Basilea Problema di Cauchy problema di cinematica problema di Collatz problema di inseguimento problema di Keplero problema di steiner problemi problemi additivi classici problemi matematici minori problemi svolti di Fisica 1 problemi unidimensionali procedimento di ortonormalizzazione di Gram-Schmidt processi aleatori processi cognitivi Processi d’urto processi deterministici processi ergodici processi stazionari processi stocastici processo aleatorio processo cicliclo processo di guarigione processo di wiener processo ergodico processo sistemico prodotti di fissione prodotti infiniti prodotto cartesiano prodotto combinatorio prodotto di applicazioni prodotto di eulero prodotto di infinitesimi prodotto hermitiano prodotto interno prodotto misto prodotto righe per colonne prodotto scalare prodotto tensoriale prodotto tensoriale di due spazi vettoriali prodotto vettoriale prof. Tauraso profezia maya profondità profotto vettore progettisti software progetto aleph Programmazione programmazione dinamica Programmazione lineare programmazione lineare intera progressioni proiettile proiettili proiettore proiezione proiezione di lambert proiezione ortogonale proiezioni ortogonali prolungamento analitico prolungamento di una funzione prolungando per continuità proof proof – La prova Propagazione di onde elettromagnetiche in un mezzo dispersivo propagazione ondosa propositional calculus proposizioni atomiche proposizioni composte proprietà proprietà additiva proprietà affini del piano proprietà antisimmetrica Proprietà associativa proprietà associativa del prodotto di applicazioni proprietà commutativa proprietà di invarianza del differenziale totale proprietà distributiva proprietà riflessiva proprietà simmetrica proprietà transitiva protone Prova di autovalutazione prova di matematica prove d’esame pseudo-ipersfera pseudoprimi di Lucas psicanalisi psichedelia puleggia puleggia ideale pulsar del granchio pulsazione punti punti allineati punti angolosi punti angolosi – punti cuspidali punti critici punti critici dell’energia punti critici di una funzione di più variabili punti cuspidali punti di aderenza punti di arresto asintotici Punti di curvatura e punti di flesso delle curve piane Punti di discontinuità Punti di discontinuità di prima specie punti di discontinuità di seconda specie Punti di discontinuità di una funzione di due variabili Punti di discontinuità eliminabile Punti di discontinuità eliminabili punti di discontinuità non eliminabile punti di equilibrio punti di flesso punti di flesso a tangente obliqua punti di flesso a tangente verticale punti di inversione punti di regresso punti di sella punti di singolarità Punti di svolta di un’orbita. Pericentro e Apocentro punti estremali punti estremanti punti mediani punti multipli punti singolari punti stazionari punto punto alfa punto all’infinito Punto angoloso punto base punto cuspidale punto di accumulazione punto di aderenza punto di discontinuità punto di discontinuità di prima specie punto di discontinuità eliminabile punto di flesso Punto di flesso a tangente verticale punto di frontiera punto di osculazione punto di sella punto doppio punto esterno punto interno punto isolato punto materiale punto multiplo punto omega punto singolare punto stazionario puntoni Pursuit problem quaderni americani quadrangolo completo quadrato quadri quadriche quadrilatero quadrilatero ciclico quantità di calore quantità di moto quanto d’azione quanto di luce quantum bit quantum bouncing ball quantum computing quantum dots quantum gravity Quantum thieves quarkonio quarta dimensione quesito natalizio quiete quiete relativa quod initium est gradatim desinendi quote quoziente di Rayleigh R con zero R0 racconti racconto radar radar ranging radiazione di fondo cosmica radiazione di fondo cosmico radiazione termica radiazione ultravioletta radicali liberi radice quadrata radici radici equazione di secondo grado radius raggio di curvatura raggio di luce raggio vettore ramanujan rampa di scale random walk range rango rango 2 rango di un tensore rango di una matrice rapporto rapporto di moderazione Rapporto incrementale rapporto rischi/benefici del vaccino anti-covid rapprasentazione parametrica rappresentazione implicita di curve piane rappresentazione in base 3 rappresentazione integrale rappresentazione naturale Rappresentazione naturale di una curva regolare rappresentazione parametrica rappresentazione parametrica del cilindro Rappresentazione parametrica della retta nel piano rappresentazione parametrica di una curva rappresentazione parametrica di una curva piana Rappresentazione parametrica di una superficie rappresentazione parametrica non regolare rappresentazione parametrica regolare Rappresentazione parametriche equivalenti rappresentazione ternaria rCBR realismo fantastico realismo fisico realtà reattore nucleare reattore nucleare termico spoglio Reattore termico eterogeneo reattore termico omogeneo reattori lenti reattori veloci reazione normale reazione vincolare reazioni avverse reazioni vincolari recipiente reciproca parte intera red shift reduce regime lineare regione accessibile regione classicamente accessibile regione non semplicemente connessa regionplot regola del parallelogramma regola di De L’Hopital regola di de l’hospital Regola di derivazione – funzioni composte Regola di derivazione – rapporto regola di l’hospital regola di Ruffini regolarità regolatore a sfere centrifughe Regole di derivazione Regole di derivazione – funzioni composte regole di derivazione covariante regressione gaussiana regula falsi regular curve Regular curve. Intrinsic tria regular curves relatività generale relatività ristretta relatività speciale relazione relazione di completezza relazione di equipollenza Relazione di equivalenza relazione di inclusione relazione di indeterminanzione tempo-energia relazione di indeterminazione tempo energia relazione di parallelismo relazione di perpendicolarità relazione identica relazione in un insieme Relazione inversa relazioni relazioni di equivalenza Relazioni in un insieme Removable discontinuity Renato Caccioppoli Renato Fiorenza rendimento rendite reparametrization of a curve Repellente ad ultrasuoni Repunit residui resistenza resistenza dell’aria resistenza differenziale resistenza dinamica resistenza elettrica resistenza passiva resistore resistori in parallelo resto di cauchy resto di lagrange resto di ordine p restrizione di una funzione resurrezione rete rete di indra rete di spin rete sociale reti autopoietiche reti lineari reti neurali reti neuronali retta retta critica Retta dei minimi quadrati retta isotropa retta normale retta normale ad una superficie retta orientata retta reale retta reale estesa retta tangente retta tangente a una curva piana data in forma implicita Retta tangente ad una curva piana retta tangente e retta normale a una curva data in forma implicita rettangolo rettangoloide rettangoloide generalizzat rettangoloide generalizzato rette caratteristiche rette complanari rette e piani rettificazione di una curva ricchezza ricerca operativa ricevitore ottico Richard Feynman ricoprimento ricorsione ricorsività ricorsività globale ricorsività locale ridotta n-esima riduzione riduzione della massa riduzionismo riemann Riemann hypothesis riferimento curvilineo riflettori rimorchio riparametrizzazione riparametrizzazione di una curva regolare ripetibilità ripetizioni di analisi matematica ripetizioni di matematica ripetizioni matematica ripetizioni online risonanza risultante ritmo cardiaco Robert Gilmore robert silverberg robot Roger Penrose roma rondella rosa a n foglie rossi RotationTransform rotazione rotazione terrestre rotazione uniforme rotazioni rotor rotore rotta rottura rottura di simmetria Round RSA Rt Rudi Rucker rudy rucker rumore bianco rumore brown ruote rutherford sakurai salita salita esponenziale salto di discontinuita salto quantico salvatore esposito sampling sandwich theorem sara Sars Co V2 sasso satellite satelliti artficiali satelliti artificiali sbarra elastica scacchi scala di infinitesimi di ordine indeterminato Scala di infiniti di ordine indeterminato scala microscopica scala mobile scalari scambio di calore scarpe scattering scattering isotropo schaum Schaum’s Outline of Differential Geometry schema di calcolo schizofrenia schrödinger schrödinger’s cat Schwarz’s Theorem scientific workplace scientificworkplace scientismo scienza scienza delle costruzioni scienze delle costruzioni scimmie scomposizione scribd scrittore transrealista sculating plane seconda forma dell’equazione delle orbite seconda guerra mondiale seconda legge di keplero seconda legge di newton seconda proiezione secondo principio della dinamica secondo principio della termodinamica secondo principio di Kirchhoff secondo teorema di cauchy segmenti segmenti equipollenti segmento segnale segnale sinusoidale segnali aleatori segnali deterministici segnali luminosi segno di una funzione self energia gravitazionale self energia gravitazionale di una stella Self-Organization semigruppi semiperimetro seno seno iperbolico seo separazione di variabili separitrici serbatoi Serie serie a termini di segno costante serie a termini positivi serie assolutamente convergente serie assolutamente convergenti serie binomiale serie convergente ma non assolutamente convergente serie delle derivate serie di Dirichlet Serie di Dirichlet. La funzione zeta di Riemann-Eulero e la funzione di Riemann-Siegel Serie di Fourier Serie di funzioni serie di funzioni non uniformemente convergente serie di laurent serie di Mac Laurin Serie di Taylor serie esponenziale serie geometrica serie iperboliche serie logaritmica” serie numerica Serie numerica con n fattoriale (n!) serie numeriche serie RC serpente a sonagli settore seno iperbolico settore tangente iperbolica sezione aurea sezione d’urto sezione d’urto macroscopica sezione trasversale sezioni sfera SHURDLU signal processing silicio sillabazione siluro simba simboli di Christoffel simbolo di Levi-Civita simbolo di peano similitudine simmetria simmetrie Simon Singh simplesso simultaneità degli eventi sin sincronicità sincronicity sincronizzazione di orologi singolari Singolarità Singolarità isolate singolarità spaziotemporale singoletto singular point Singular point of the cissoid sintesi armonica sintropia sistema autogravitante sistema del centro di massa sistema del laboratorio Sistema di ascisse curvilinee sistema di coordinate in co-moving sistema di equazioni lineari sistema di generatori sistema di navigazione inerziale Sistema di riferimento inerziale sistema di riferimento non inerziale sistema di riferimento rotante sistema di riferimento sincrono sistema di vettori applicasti sistema fondamentale di integrali sistema formale sistema inerziale sistema isolato sistema lineamente dipendente sistema lineare sistema massimo linearmente indipendente sistema meccanico sistema non lineare sistema ortonormale sistema ortonormale completo sistema quantistico unidimensionale sistemi a tempo discreto sistemi autonomi sistemi autopoietici sistemi caotici sistemi conservativi undimensionali sistemi di computer algebra Sistemi di disequazioni Sistemi di equazioni lineari sistemi di equazioni lineari incompatibili sistemi di funzioni iterate sistemi di numerazione sistemi di punti materiali sistemi di telecomunicazione sistemi dinamici sistemi dinamici a tempo discreto sistemi dinamici autonomi Sistemi dinamici autonomi lineari sistemi dinamici iterati sistemi dinamici lineari sistemi dinamici non lineari sistemi hamiltoniani sistemi lineari sistemi lineari omogenei sistemi olonici sistemi olonomi sistemi passivi sistemi termodinamici sistemi viventi six young men smart smartwatch smirnov SMP sngular points Software software computer algebra sogni sogni di robot sogno solaris sole solenoidale solenoide solido di rotazione solitone solitoni soluzione di D’Alembert soluzioni in forma implicita soluzioni locali solve somma somma di due variabili Somma di Eulero somma di funzioni somma di infinitesimi somma di infiniti segmenti somma di una serie somma di variabili somma diretta Somma diretta di sottospazi somma integrale somma parziale di ordine n sommabilità sommatoria somme di Riemann somme integrali sommergibile sommergibili sonar sonda Sophie Germain sostema di coordinate sincrono sostituzione sostituzione di parametro ammissibile sostituzione universale di variabile sostituzioni di eulero sostituzioni iperboliche Sostituzioni trigonometriche sostituzioni trigonometriche ed iperboliche sosttospazio vettoriale sottocriticità sottoinsiemi sottospazio sottospazio invariante sottospazio vettoriale sovrapposizione degli stati spaccio di cocaina sparpagliamento Spazi compatti spazi di banach spazi di bell Spazi di funzioni Spazi di Hausdorff spazi di Hilbert spazi di prodotto scalare spazi euclidei spazi infinite dimensioni spazi metrici spazi propriamente euclidei spazi pseudoeuclidei spazi topologici spazi vettoriali spazi vettoriali unitari spazio spazio affine spazio assoluto spazio biduale spazio complesso spazio connesso spazio della mente spazio delle configurazioni spazio di hausdorff spazio di hilbert spazio duale spazio duale di uno spazio vettoriale spazio e tempo spazio euclideo spazio funzionale spazio intersezione spazio metrico spazio normato spazio nullo spazio polinomi spazio pseudoeuclideo spazio sconnesso spazio tempo spazio topologico spazio unitario spazio vettoriale spazio vettoriale dei polinomi spaziotempo speranza matematica spettro spettro continuo spettro del corpo nero spettro di fourier spettro di potenza spettroscopio spezzata spiagge spiegel spin spin network spin networks spin zero SPION spirale di archimede spirale di cotes spirale logaritmica spoletta Srinivasa Ramanujan Alyanger stabilità asintotica stabilità assoluta stabilità dei sistemi di controllo stabilità delle orbite circolari Stabilità di Lyapunov stabilità di un reattore nucleare stabilità secondo Lyapunov stan wagon stanislav grof stantuffo star trek stati alterati di coscienza stati antisimmetrici stati coerenti stati ghost stati ghosti stati legati stati simmetrici stati stazionari statica statistica statistica bayesiana statistica biomedica statistica di fermi dirac statistica di poisson statistiche quantiche statistiche quantistiche stato fondamentale stato termodinamico stazione spaziale stella stelle Stephen Hawking Stephen Wolfram steve jobs steve wozniak steven levy steven weinberg storia Storia di John Nash strange loop strange loops strani anelli strati cilindrici strati piani strofoide struttura a nastro struttura stellare strutture algebriche strutture dati Stuart Kauffman studio della studio della convergenza/divergenza di una serie numerica Studio della funzione Studio delle funzioni studio di funzione successione di fibonacci successione divergente successione infinitesima successioni successioni convergenti successioni di funzioni successioni divergenti successioni indeterminate successioni non regolari Successioni per ricorrenza successioni ricorsivamente definite successioni ricorsive successioni univocamente definite suicidio superconduttività supercoscienza supercriticità superfice non orientabile superfice orientabile superfici superfici di livello superfici ortogonali superfici parallele superfici piane superfici tangenti superficie superficie di livello superficie equipotenziale superficie non orientabile superficie orientabile superficie regolare superficie unilatera supernova supernove lontane supplementare supplementare ortogonale Sviluppi asintotici sviluppo asintotico sviluppo di Fourier sviluppo di hadamard sviluppo di taylor sviluppo in serie sviluppo in serie di Fourier sycamore Syllabus tabelle table tabular tachioni tale supporto garantisce una condivisione più efficiente. talete tamponi tangente tangente iperbolica Tangential acceleration and normal acceleration (Analytical Mechanics) tao della fisica taosimo tarsky tartaruga tassellatura del piano tassellature tasselletura del piano tasselli tasso di contagio tasso di contagio effettivo tautocrona tautocronia tavolo tecnodo teflon Teletrasporto temperatura temperatura calorica temperatura di congelamento temperatura di equilibrio temperatura di regime temperatura media di un fluido tempo tempo assoluto tempo caratteristico tempo compton tempo di Hubble tempo di incubazione tempo di planck tempo di volo tempo in meccanica classica tempo proprio tennista tensione tensore tensore covariante tensore covariante di rango 2 tensore di Kronecker tensori tensori completamente antisimmetrici tensori completamente simmetrici tensori controvarianti tensori controvarianti di rango r tensori covarianti tensori misti tensori misti di rango 2 teorema Teorema cinese del resto teorema degli zeri Teorema dei carabinieri teorema dei numeri primi teorema dei quattro colori Teorema dei residui teorema del coriolis Teorema del Delirio teorema del differenziale totale teorema del Dini teorema del lavoro e dell’energia cinetica teorema del limite teorema del limite e teorema della continuità per le serie di funzioni teorema del matrimonio teorema del momento della quantità di moto Teorema del momento della quantità di moto per un sistema di punti materiali teorema del piccolo guadagno teorema del punto fisso Teorema del sandwich teorema del varignon teorema della divergenza teorema della divergenza nel piano teorema della funzione implicita teorema della media teorema della media integrale teorema delle forze vive teorema di Bayes teorema di bell Teorema di Bolzano-Weierstrass Teorema di Brocard teorema di brouwer teorema di cambridge teorema di cauchy-lipschitz Teorema di Chebyshev Teorema di Commandino teorema di continuità teorema di coriolis teorema di cramer Teorema di decomposizione spettrale Teorema di derivazione per serie Teorema di divisione euclidea teorema di equipartizione dell’energia teorema di esistenza teorema di esistenza e unicità teorema di esistenza ed unicità teorema di euclide teorema di Fermat teorema di gauss teorema di gauss green Teorema di Girard teorema di gödel Teorema di Green Teorema di Guldino Teorema di Helmholtz teorema di integrazione per serie teorema di inversione locale Teorema di König teorema di L’Hospital teorema di lagrange teorema di liouville Teorema di Maschke teorema di menelao teorema di napoleone teorema di oxford Teorema di Paley-Wiener teorema di Pitagora teorema di Plancherel teorema di riesz teorema di rolle Teorema di Rouche Capelli Teorema di Schwarz Teorema di Simson teorema di stewart Teorema di Stokes teorema di Sylvester teorema di torricelli-barrow Teorema di unicità del limite teorema di Weierstrass Teorema di Wiener Khintchine teorema esistenza ed unicità teorema faltung teorema fondamentale del calcolo integrale teorema fondamentale dell’algebra Teorema Fondamentale dell’Aritmetica Teorema no-signaling teorema notevole teorema spettrale teorema sulla somma di limiti teoremi teoremi di De L’Hospital teoremi di Fermat e Wilson teoremi di gödel teoremi di Lyapunov e di Cetaev Teoremi di Rolle – Lagrange – Cauchy Teoria degli insiemi teoria dei giochi Teoria dei Grafi teoria dei grandi numeri di Dirac teoria dei gravitini teoria dei gruppi Teoria dei numeri teoria dei segnali teoria dei semigruppi teoria dei sistemi teoria dei sistemi dinamici teoria del campo di ordinamento teoria del potenziale teoria del trasporto teoria dell’integrazione teoria della gravitazione teoria della gravitazione di Newton teoria delle curve teoria delle distribuzioni teoria delle perturbazioni Teoria delle Stringhe teoria di Brans-Dicke teoria di jeans Teorie di Stringa termine di ordine inferiore termine di ordine superiore termodin Termodinamica termodinamica assiomatica terna destrogira terna levogira terna terrestre terne destrogire terne di goldbach terne levogire Terne pitagoriche terno al lotto terra terra sferica terrapiattisti Terry Winograd terza legge di keplero terza legge di newton terzo principio della dinamica tessere di penrose test Test di primalità testata nucleare tetraedro tetto texnic The Science of Healing Revealed The structure of scientific revolution The turning point the web of life theory of everything thomas fermi Thomas S. Kuhn tigre time machine puntiforme tipologie di materiali superconduttori tiranti tiro alla fune titolo tombola topologia topologia banale topologia discreta toro toro aperto torre di pisa torsione Tossicità farmacologica e white noise traccia di una matrice traiettoria traiettoria deterministica traiettorie ortogonali traiettorie patologiche tram tramissione del calore per convezione tramsissione del calore transitiva transitori cellulari transitorio transitorio circuitale Transrealismo trapezio trapezio curvilineo trascendente intera Trasformata di Fourier Trasformata di Laplace trasformata discreta di Fourier trasformazione conforme trasformazione di Joukowsy trasformazione di variabili Trasformazione lineare aggiunta trasformazione termodinamica trasformazioni di lorentz trasformazioni galileiane trasformazioni lineari traslazione traslazione temporale trasmissione dei segnali trasmissione del calore trasmissione di calore trasmissione di calore per irraggiamento trasporto trasporto neutroni trasporto parallelo trattore tre mondi treni trenino giocattolo treno treno azionato dalla gravità Triangoli di Kanizsa triangolo triangolo curvilineo triangolo di penrose triangolo di sierpinski triangolo di Tartaglia triangolo equilatero triangolo rettangolo Triangolo somma pari Triedro principale Trigonometria trigonometria piana trinomio di secondo grado trivial zeros Tsunami tubo di venturi tuffatore turbina pelton tutorato Tuttavia u-boat uccellino uccello ucciderò il gatto di Schrödinger uguaglianza di parseval uguaglianza di vettori uguaglianza geometrica uguaglianza logica ultimo teorema di fermat ultrasuoni umidità Un matematico di nome H Un matematico è una macchina che converte caffè in teoremi Unified Modeling Language union unione unit step unità immaginaria unitstep universi di gödel universi paralleli Università degli Studi di Napoli Federico II università di bologna universo universo 25 universo di darling universo primordiale universo stazionario uno elevato a infinito uomo uova strapazzate uovo crudo uovo sodo urania uranio uranio 235 uranio arricchito uranio naturale uranium urna urto urto anelastico urto completamente anelastico urto elastico urto endoenergetico urto esoenergetico urto fotone elettrone urto nello spazio urto normale centrale urto perfettamente anelastico User Group Meeting vacanze vaccini vaccino vagoni valerio brunetti valor medio Valore assoluto valore assoluto di una funzione valore assoluto di una funzione tende all’infinito valore di plateau valore efficace valutazione di probabilità vapor d’acqua vapore vapore d’acqua varela variabile aleatoria variabile deterministica variabile gaussiana variabili aleatorie variabili artificiali variabili deterministiche variabili ergodiche variabili separabili variante delta varianti variazione di entropia varietà Varietà affine varietà differenziabile varietà pseudoriemanniana varietà topologica veleni velivolo velocista velocità velocità aereolare velocità angolar velocità angolare velocità assoluta velocità del suono velocità della luce velocità della luce nel vuoto velocità di fase velocità di gruppo di un pacchetto d’onde velocità di lancio velocità di trascinamento velocità iniziale velocità limite velocità limite di una paracadutista velocità media velocità radiale velocità relativa velocità scalare velocità scalare media velocità trasversale velocità vettoriale media velore efficace ventilatore da condotta ventilatore da condotto verità scientifica Véronique Malard verso di percorrenza versore versore normale vettore vettore bre vettore di stato vettore ket vettore libero ordinario vettore posizione vettore tangente vettore tangente a una curva vettore unitario vettore velocità vettori vettori applicati vettori bra vettori complanari vettori controvarianti vettori covarianti vettori in R^3 vettori ket vettori linearamente indipendenti vettori linearmente dipendenti vettori linearmente indipendenti vettori ortogonali vettori paralleli vettori proporzionali via panisperna viaggi nel tempo vibrazioni vibrazioni trasversali video lezioni vincolo vinogradov virologia virus virus biologici virus informatici virus mutato viscosità volume volume costante Volume del toro volume parallelepipedo volume piramide Volume solido di rotazione von neumann vortici voti vuoto vuoto quantistico vuoto quanto-meccanico watt wavelets web of life Weierstrass well-posedness del problema werner heisenberg wheeler which white noise whitenoise wiener william gibson wilson wired wolfang pauli wolfgang pauli wolfram woodall wordpress working precision wormhole WYSIWYG Yoichi Miyaoka youtube zangrillo zen zeri zeri della funzione di riemann zeri della funzione zeta di riemann zeri di una funzione zeri funzione zeta di riemann zeri non banali zeri non banali zeta di riemann zeri semplici zeta di Keith zeta di riemann

Tags: prolungamento di una funzione, restrizione di una funzione

Articoli correlati