[¯|¯] Programmi ricorsivi con Mathematica: il Teorema di Euclide

Agosto 29th, 2014 | by extrabyte |

Nel post precedente abbiamo esaminato la possibilità dell'utilizzo di tecniche di cashing per ridurre il carico computazionale di un programma scritto in ambiente Mathematica.

Applichiamo, ora, tale tecnica al Teorema di Euclide, noto anche come Teorema dell'infinità dei numeri primi. Secondo tale teorema detto p_n l'ennesimo numero primo.... Precisamente:

Teorema di Euclide
Hp. 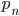$p_{n}$ è l'n-esimo numero primo,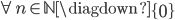 $\forall n\in\math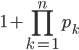bb{N}\diagdown\left\{ 0\right\}$

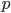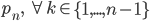
Th. $1+{\displaystyle\prod\limits_{k=1}^{n}}p_{k}$ se non è primo ha un fattore $p$ > $p_{n},\,\,\,\forall k\in\left\{ 1,...,n-1\right\}$

Ciò implica l'esistenza di un numero infinito di numeri primi.

A questo punto ricordiamo che Mathematica ha le seguenti funzioni built-in per il calcolo di numeri primi: Prime[n] restituisce l'n-esimo numero primo; PrimePi[n] restituisce il numero di primi minori o uguali a n.

Con Mathematica il prodotto 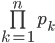${\prod\limits_{k=1}^{n}}p_{k}$ , è calcolato dall funzione ricorsiva:

Per il teorema di Euclide 1 + f[n] se non è primo ha un fattore primo 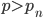$p>p_{n}$ . Possiamo creare la lista

Per ridurre il carico computazionale possiamo utilizzare la tecnica cashing, definendo la funzione ricorsiva come:

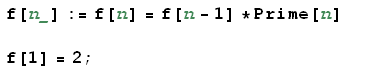
per poi generare la lista precedente e confrantando i tempi di calcolo con il comando Timing. Dobbiamo, però, far notare che con i processori odierni, la differenza di tempo di calcolo è del tutto trascurabile.