[¯|¯] Derivata secondo una direzione (di una funzione vettoriale)

Febbraio 6th, 2020 | by Marcello Colozzo |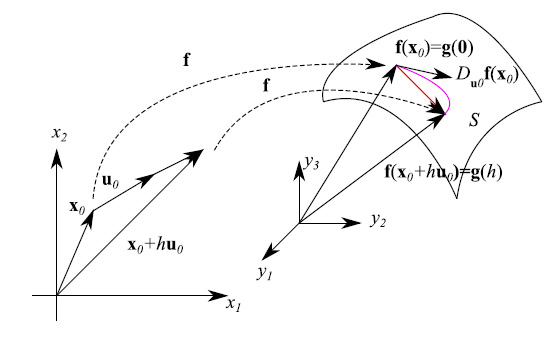

derivata secondo una direzione,rapporto incrementale,funzione vettoriale — **Fig. 1**

A questo link è diponibile una dispensa sulle funzioni vettoriali continue. Passiamo ora alla derivata secondo una direzione.

Definizione
Siano E,F spazi vettoriali su uno stesso campo K. Assegnata una funzione vettoriale f(x) definita in sottoinsieme non vuoto di E, e un vettore u₀ di E -{0}definiamo il rapporto incrementale di f(x) in x₀ nella direzione di u₀, il seguente vettore

Il predetto rapporto è una funzione vettoriale della variabile scalare h, definita in K-{0}, ove manifestamente h=0 è punto di accumulazione per tale insieme di definizione. Quindi possiamo studiare il comportamento della funzione in un intorno di detto punto.

Definizione
Se il rapporto incrementale converge per h->0, diremo che la funzione vettoriale f(x) è derivabile
nel punto x₀ e secondo la direzione del vettore u₀. Inoltre, posto

e il primo membro, i.e. il limite del rapporto incrementale, si chiama derivata di f in x₀ secondo la direzione di u₀.

Osserviamo che per un assegnato x₀ di V, f(x₀+hu₀) è una funzione vettoriale della variabile scalare h. Definiamo:

Segue, con ovvio significato dei simboli:

Tali conclusioni si prestano a una interpretazione geometrica. A tale scopo, consideriamo il caso speciale:

Ne consegue che y=f(x) è la rappresentazione parametrica di una superficie, come illustrato in fig. 1. Qui vediamo che il rapporto incrementale è il vettore rappresentato in rosso. Inoltre, al variare del parametro h, l'equazione vettoriale x=x₀+hu₀ descrive una retta r di R² per il punto posizionato da x₀, e parallela al vettore u₀. Ne segue che

è l'immagine di r attraverso f o ciò che è lo stesso attraverso g. Questa immagine è una curva γ di rappresentazione parametrica y=g(h), per cui il vettore g'(0) è tangente a γ in g(0)=f(x₀).

No TweetBacks yet. (Be the first to Tweet this post)